
【题目】在正方形ABCD中,点E、F在边AB、CD上,点G、H在边AD、CB上,EF和GH相交于点O,∠DGH=70°,按下列要求分别画出EF

(1)当∠GOE=90°时,求证:EF=GH;
(2)当EF=GH时,画出示意图,直接写出∠GOE的度数.
【答案】(1)见解析;(2)见解析,∠GOE=90°或50°.
【解析】
(1)作ET⊥CD于T,作HR⊥AD于R,构造两个直角三角形,利用正方形四边相等,四个角都是直角,且∠GOE=90°,证明这两个直角三角形全等,即可;
(2)同理,构造两个直角三角形,利用正方形四边相等,四个角都是直角,且EF=GH,证明这两个直角三角形全等,即可求得答案.要注意EF与GH的两种不同的相交情况.
解:(1)如图1,过点E作ET⊥CD于T,过点H作HR⊥AD于R,
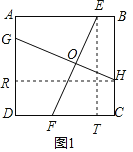
则∠ETF=∠HRG=90°
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠B=∠C=∠D=90°,AB∥CD,AD∥BC
∴四边形ABHR、四边形BCTE均为矩形
∴HR=AB=BC=ET
∵∠GOE=90°
∴∠GOF=90°,∠GOF+∠D=180°
∵∠DGO+∠DFO+∠GOF+∠D=360°
∴∠DGO+∠DFO=180°
∵∠EFT+∠DFO=180°
∴∠DGO=∠EFT
∴△EFT≌△HGR(AAS)
∴EF=GH;
(2)如图2,过点E作ET⊥CD于T,过点H作HR⊥AD于R,
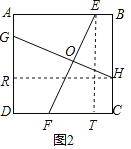
则∠ETF=∠HRG=90°
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠B=∠C=∠D=90°,AB∥CD,AD∥BC
∴四边形ABHR、四边形BCTE均为矩形
∴HR=AB=BC=ET
∵EF=GH
∴Rt△EFT≌Rt△HGR(HL)
∴∠EFT=∠HGR
∵∠EFT+∠DFO=180°
∴∠HGR+∠DFO=180°
∵∠HGR+∠DFO+∠GOF+∠D=360°
∴∠GOF+∠D=180°
∴∠GOF=90°
∴∠GOE=90°
如图3,过点E作ET⊥CD于T,过点H作HR⊥AD于R,
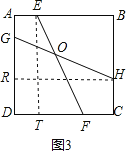
则∠ETF=∠HRG=90°
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠B=∠C=∠D=90°,AB∥CD,AD∥BC
∴四边形ABHR、四边形BCTE均为矩形
∴HR=AB=BC=ET
∵EF=GH
∴Rt△EFT≌Rt△HGR(HL)
∴∠EFT=∠HGR=70°
∵∠HGR+∠DFO+∠GOF+∠D=360°
∴∠FOG=130°
∴∠GOE=180°﹣∠FOG=180°﹣130°=50°
综上所述,∠GOE=90°或50°.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P的坐标为(2a+6,a-3)
(1)当点P的纵坐标为-4,求a的值;
(2)若点P在y轴上,求点P的坐标;
(3)若点P在第四象限,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请按要求完成下面三道小题(本题作图不要求尺规作图).
(1)如图1,AB=AC.这两条线段一定关于∠BAC的______所在直线对称,请画出该直线.
(2)如图2,已知线段AB和点C.求作线段CD,使它与AB成轴对称,且A与C是对称点,对称轴是线段AC的______.
(3)如图3,任意位置(不成轴对称)的两条线段AB,CD,AB=CD.你能从(1),(2)问中获得的启示,对其中一条线段作两次轴对称使它们重合吗?如果能,请画出图形并简要描述操作步骤;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,E、F是四边形ABCD的对角线AC上的两点,且AF=CE,DF=BE,DF∥BE.

(1)求证:△CDF≌△ABE;
(2)求证:四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为线段
为线段![]() 上一动点,分别过点
上一动点,分别过点![]() 作
作![]() ,
,![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的值;
的值;
(2)探究:当点![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?最小值是多少?
的值最小?最小值是多少?
(3)根据(2)中的结论,请构造图形求代数式![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级某班级部分同学去植树,若每人平均植树7棵,还剩9棵,若每人平均植树9棵,则有1位同学植树的棵数不到8棵.若设同学人数为x人,植树的棵数为(7x+9)棵,下列各项能准确的求出同学人数与种植的树木的数量的是( )
A. 7x+9≤8+9(x﹣1) B. 7x+9≥9(x﹣1)
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com