
����Ŀ���밴Ҫ�������������С�⣨������ͼ��Ҫ��߹���ͼ��.
��1����ͼ1��AB=AC.�������߶�һ�����ڡ�BAC��______����ֱ�߶Գƣ��뻭����ֱ��.
��2����ͼ2����֪�߶�AB�͵�C.�����߶�CD��ʹ����AB����Գƣ���A��C�ǶԳƵ㣬�Գ������߶�AC��______.
��3����ͼ3������λ�ã�������Գƣ��������߶�AB��CD��AB=CD.���ܴӣ�1������2�����л�õ���ʾ��������һ���߶���������Գ�ʹ�����غ�������ܣ��뻭��ͼ�β���Ҫ�����������裻������ܣ���˵������.

���𰸡���1����ƽ���ߣ���ͼ����������2����ֱƽ���ߣ���ͼ����������3���ܣ���ͼ������.
��������
��1��������Գ���������BAC�Ľ�ƽ�����ɣ���2������AC����AC�Ĵ�ֱƽ���ߣ���Ϊ�Գ��ᣬ��B����ڶԳ���ĶԳƵ�D������CD��Ϊ����3������BD����BD�Ĵ�ֱƽ���ߣ���Ϊ�Գ��ᣬ����C���ڶԳ���ĶԳƵ�E������BE������ABE�Ľ�ƽ����Ϊ�Գ��ᣬ���ɶ�����һ���߶���������Գ�ʹ�����غ�.
��1����ͼ������BAC�Ľ�ƽ���ߣ����ǡ�BAC�ĶԳ��ᣬ
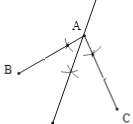
�ʴ�Ϊ����ƽ����
��2����ͼ������AC����AC�Ĵ�ֱƽ���ߣ���Ϊ�Գ��ᣬ��B����ڶԳ���ĶԳƵ�D������CD��Ϊ����.
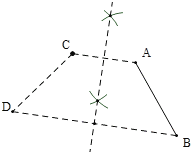
�ʴ�Ϊ����ֱƽ����
��3������BD����BD�Ĵ�ֱƽ���ߣ���Ϊ�Գ��ᣬ����C���ڶԳ���ĶԳƵ�E������BE������ABE�Ľ�ƽ����Ϊ�Գ��ᣬ
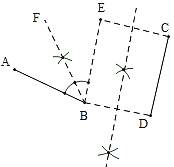
���ܶ�����һ���߶���������Գ�ʹ�����غ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABΪ��O��ֱ����BD��CDΪ��O�����ߣ��е�ֱ�ΪB��C��
��1����֤��AC��OD��
��2����BC=BD����BD=6cmʱ����ͼ����Ӱ���ֵ�����������ȡ����ֵ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ױ�BC�ij�Ϊ4�����Ϊ12����AB�Ĵ�ֱƽ����EF��AB�ڵ�E����AC�ڵ�F.��DΪBC�ߵ��е㣬MΪ�߶�EF��һ�����㣬����BDM���ܳ�����СֵΪ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij��ʵʩ���д����Ĺ����У�����������Ǩ���̶ӳа���һ��10000 m2�IJ�Ǩ���̣�������������֣�ʵ�ʲ�ǨЧ�ʱ�ԭ�ƻ������25%����ǰ2����������������������⣺
��1��������������Ǩ���̶�����ƽ��ÿ���Ǩ����ƽ���ף�
��2��Ϊ�˾������ٲ�Ǩ����������IJ��㣬�ڲ�Ǩ����������2�������������Ǩ���̶ӵ��쵼�����ӿ��Ǩ�����������µIJ�Ǩ������5������ɣ���ô����������Ǩ���̶�ƽ��ÿ�������ٶ��Ǩ����ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���н����ֶ�����Ϊ�˵���ѧ��������Լ���������ݵ��˽�̶ȣ��̶ȷ֣���![]() �˽�ܶ�������
�˽�ܶ�������![]() �˽�϶�������
�˽�϶�������![]() �˽����������
�˽����������![]() ���˽��������Ա���ij����ѧ��ѧ�������˳������飬���ǽ���ε���Ľ����������������������ͳ��ͼ.
���˽��������Ա���ij����ѧ��ѧ�������˳������飬���ǽ���ε���Ľ����������������������ͳ��ͼ.

����������Ϣ�����������.
��1����ȫ����ͳ��ͼ.
��2�����γ��������˶�����ѧ����������ͳ��ͼ�У�����![]() ����Ӧ��Բ�ĽǵĶ���.
����Ӧ��Բ�ĽǵĶ���.
��3������ѧ����2000��ѧ�����������������ѧ������ѧ���У�������Լ�������������˽���������ж�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��1��a���Ƿ���������![]() ��ͼ����һ����ֱ��
��ͼ����һ����ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ��Ľ���Ϊ��B��D����B��3����1��������
��ͼ��Ľ���Ϊ��B��D����B��3����1��������
��1�����������Ľ���ʽ��
��2�����D��������ֱ��д��y1��y2ʱx��ȡֵ��Χ��
��3������P��x��0����x������������˶������߶�PA���߶�PB֮��ﵽ���ʱ�����P��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У���E��F�ڱ�AB��CD�ϣ���G��H�ڱ�AD��CB�ϣ�EF��GH�ཻ�ڵ�O����DGH��70����������Ҫ��ֱ�EF

��1������GOE��90��ʱ����֤��EF��GH��
��2����EF��GHʱ������ʾ��ͼ��ֱ��д����GOE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��1500��ѧ����Ϊ�˽�ȫУѧ������ѧ��ʽ����У��ѧ��ȤС����ȫУ�����ȡ��100��ѧ�����г������飮�����������ݣ��õ�����ͼ����Ƶ���ֲ����в��ֻ��DZ�īˮ��ס����
ijУ100��ѧ����ѧ��ʽƵ���ֲ���
��ʽ | ���� | Ƶ�� |
���� | ������ | 15 |
�ﳵ | ���������� | 29 |
�˹�����ͨ���� | ������������ | 30 |
��˽�ҳ� | ||
���� | ||
�ϼ� | 100 |
��1�����ε���ĸ������� ����
��2����Ƶ���ֲ����У�����˽�ҳ������ֶ�Ӧ��Ƶ����
��3������Ƹ�У1500��ѧ���У�ѡ���ﳵ���˹����Ͳ�����ѧ��һ���ж����ˣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com