练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，等腰三角形ABC底边BC的长为4，面积为12，腰AB的垂直平分线EF交AB于点E，交AC于点F.若D为BC边的中点，M为线段EF上一个动点，则△BDM的周长的最小值为______．

    【答案】8

    【解析】

    连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．

    解：如图，连接AD，

    ∵△ABC是等腰三角形，点D是BC边的中点，
    ∴AD⊥BC，∴S△ABC=BCAD=×4×AD=12，

    解得AD=6，

    ∵EF是线段AB的垂直平分线，

    ∴点B关于直线EF的对称点为点A，

    ∴AD的长为BM+MD的最小值，
    ∴△BDM的周长最短=（BM+MD）+BD=AD+BC=6+×4=6+2=8cm．


    故填：8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在五边形中，，，，在，上分别找一点，，使得的周长最小时，则的度数为（ ）.

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠AOB=125°，把△ABC剪成三部分，边AB、BCAC放在同一直线上，点O都落在直线MN上，且S△BCO：S△CAO：S△ABO=BC：CA：AB，则∠ACB的度数为（　　）

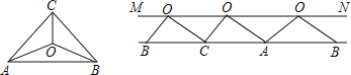
    A.70°B.65°C.60°D.85°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降，今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为90万元，今年销售额只有80万元．

    （1）今年5月份A款汽车每辆售价多少万元？

    （2）为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知B款汽车每辆进价为7.5万元，每辆售价为10.5万元，A款汽车每辆进价为6万元，若卖出这两款汽车15辆后获利不低于38万元，问B款汽车至少卖出多少辆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：若两个三角形，有两边相等且其中一组等边所对的角对应相等，但不是全等三角形，我们就称这两个三角形为偏差三角形．

    （1）如图1，已知A（3，2），B（4，0），请在x轴上找一个C，使得△OAB与△OAC是偏差三角形．你找到的C点的坐标是______，直接写出∠OBA和∠OCA的数量关系______．

    （2）如图2，在四边形ABCD中，AC平分∠BAD，∠D+∠B=180°，问△ABC与△ACD是偏差三角形吗？请说明理由．

    （3）如图3，在四边形ABCD中，AB=DC，AC与BD交于点P，BD+AC=9，∠BAC+∠BDC=180°，其中∠BDC＜90°，且点C到直线BD的距离是3，求△ABC与△BCD的面积之和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从2开始的连续偶数相加，它们和的情况如下表：

    加数的个数（n）

    和（S）

    1

    2=1×2

    2

    2+4=6=2×3

    3

    2+4+6=12=3×4

    4

    2+4+6+8=20=4×5

    5

    2+4+6+8+10=30=5×6

    …

    …

    （1）根据表中的规律，直接写出2+4+6+8+10+12+14=________

    （2）根据表中的规律猜想：S=2+4+6+8+…+2n=___________（用n的代数式表示）；

    （3）利用上题中的公式计算102+104+106+…+200的值（要求写出计算过程）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC与△CDE均是等边三角形，点B、C、E在同一条直线上，AE与BD交于点O，AE与CD交于点G，AC与BD交于点F，连接OC、FG，则下列结论：①AE=BD；②AG=BF；③FG∥BE；④∠BOC=∠EOC．其中正确结论的个数为

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

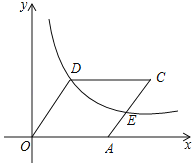
    【题目】如图，在平面直角坐标系xOy中，函数y=（k＞0，x＞0）的图象经过菱形OACD的顶点D和边AC的中点E，若菱形OACD的边长为3，则k的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E，F分别为AB，AD上的点，且AE=AF，点M是EF的中点，连结CM.

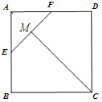
    （1）求证：CM⊥EF.

    （2）设正方形ABCD的边长为2，若五边形BCDEF的面积为，请直接写出CM的长.

    查看答案和解析>>

    同步练习册答案