Question

【题目】如图，已知△ABC与△CDE均是等边三角形，点B、C、E在同一条直线上，AE与BD交于点O，AE与CD交于点G，AC与BD交于点F，连接OC、FG，则下列结论：①AE=BD；②AG=BF；③FG∥BE；④∠BOC=∠EOC．其中正确结论的个数为

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】D

【解析】

根据题意，结合图形，对选项一一求证，即可得出正确选项．

（1）△ABC和△DCE均是等边三角形，点B，C，E在同一条直线上，∴AC=BC，EC=DC，∠ACB=∠DCE=60°，∴∠ACE=∠BCD=120°．

在△BCD和△ACE中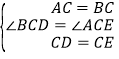，∵，∴△BCD≌△ACE，∴AE=BD，故结论①正确；

（2）∵△BCD≌△ECA，∴∠GAC=∠FBC．

又∵∠ACG=∠BCF=60°，AC=BC，∴△ACG≌△BCF，∴AG=BF，故结论②正确；

（3）∵△ACG≌△BCF，∴CG=CF．

∵∠ACB=∠DCE=60°，∴∠ACD=60°，∴△FCG为等边三角形，∴∠FGC=60°，∴∠FGC=∠DCE，∴FG∥BE，故结论③正确；

（4）过C作CN⊥AE于N，CZ⊥BD于Z，则∠CNE=∠CZD=90°．

∵△ACE≌△BCD，∴∠CDZ=∠CEN．

在△CDZ和△CEN中，，∴△CDZ≌△CEN，∴CZ=CN．

∵CN⊥AE，CZ⊥BD，∴∠BOC=∠EOC，故结论④正确．

综上所述：四个结论均正确．

故选D．