
【题目】如图,在正方形ABCD中,E,F分别为AB,AD上的点,且AE=AF,点M是EF的中点,连结CM.
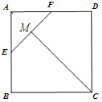
(1)求证:CM⊥EF.
(2)设正方形ABCD的边长为2,若五边形BCDEF的面积为![]() ,请直接写出CM的长.
,请直接写出CM的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连结 CE,CF,知道AE=AF,可得CE=CF,即可证明;(2)正方形ABCD的边长为2,若五边形BCDEF的面积为![]() ,则可算出△AEF的面积,从而求出CM
,则可算出△AEF的面积,从而求出CM
(1)证明:连结 CE,CF
∵四边形 ABCD 是正方形
∴∠B=∠D=90°, BC=CD AB=AD
又 AE=AF
∴BE=DF
∴△CBE≌△CDF(SAS)
∴CE=CF
而M 是 EF 中点
∴CM⊥EF(等腰三角形三线合一)
(2)连接AM,由(1)可知,AMC三点共线,
正方形ABCD的边长为2,若五边形BCDEF的面积为![]() ,则△ AEF的面积为
,则△ AEF的面积为![]() ,
,
则AC=![]() ,AE=AF=
,AE=AF=![]() ,
,
∴EF=![]() ,AM=
,AM=![]() ,则CM=
,则CM=![]() -
-![]() =
=![]()



 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
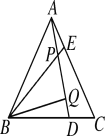
【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2) 求BE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学成绩好的同学,其计算的准确性一定还可以,七年级某班数学李老师很注重学生的计算过关检测,在学完《有理数》后,对全班同学进行检测过关.下表是这个班的童威同学一周内五天检测过关成绩(以85分为标准,高出部分用“+”表示,低于的部分用“-”表示)
星期 | 一 | 二 | 三 | 四 | 五 |
分数变化 |
|
|
|
|
|
(1)本周内童威同学哪天的检测成绩最高?是多少?哪天的检测成绩最低?是多少?
(2)请计算这5次检测成绩的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数![]() 的图象上,且x1<x2<x3,( )
的图象上,且x1<x2<x3,( )
A. 若![]() <
<![]() <
<![]() ,则
,则![]() +
+![]() +
+![]() >0B. 若
>0B. 若![]() <
<![]() <
<![]() ,则
,则![]()
![]()
![]() <0
<0
C. 若![]() <
<![]() <
<![]() ,则
,则![]() +
+![]() +
+![]() >0D. 若
>0D. 若![]() <
<![]() <
<![]() ,则
,则![]()
![]()
![]() <0
<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你阅读下列解题过程,并回答所提出的问题.
计算:![]()
解:原式=![]() ①
①
=![]() ②
②
=x-3-3(x+1) ③
=-2x-6 ④
(1)上述计算过程中,从哪一步开始出现错误______;
(2)从②到③是否正确?__________,若不正确,错误的原因是______________;
(3)请你给出正确答案__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() 互为相反数,
互为相反数,![]() 互为倒数,且
互为倒数,且![]() 的立方等于它本身.
的立方等于它本身.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 试讨论:当
试讨论:当![]() 为有理数时,
为有理数时,![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
![]() 若
若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列已知条件,分别指出两个图形中的等腰三角形,并利用第一个图证明结论。
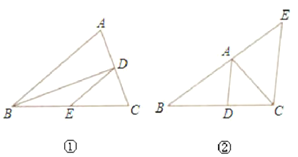
(1)如图①,BD平分∠ABC,DE//AB
(2) 如图②,AD平分∠BAC , EC//AD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com