
【题目】定义:若两个三角形,有两边相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏差三角形.
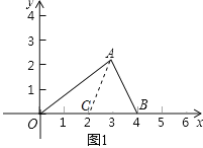
(1)如图1,已知A(3,2),B(4,0),请在x轴上找一个C,使得△OAB与△OAC是偏差三角形.你找到的C点的坐标是______,直接写出∠OBA和∠OCA的数量关系______.
(2)如图2,在四边形ABCD中,AC平分∠BAD,∠D+∠B=180°,问△ABC与△ACD是偏差三角形吗?请说明理由.
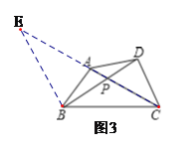
(3)如图3,在四边形ABCD中,AB=DC,AC与BD交于点P,BD+AC=9,∠BAC+∠BDC=180°,其中∠BDC<90°,且点C到直线BD的距离是3,求△ABC与△BCD的面积之和.

【答案】(1)(2,0),∠OBA+∠OCA=180°;(2)△ABC与△ACD是偏差三角形,理由见解析;(3)![]()
【解析】
(1)根据偏差三角形的定义,即可得到C的坐标,根据等腰三角形的性质和平角的定义,即可得到结论;
(2)在AD上取一点H,使得AH=AB,易证△CAH≌△CAB,进而可得∠D=∠CHD,根据偏差三角形的定义,即可得到结论;
(3)延长CA至点E,使AE=BD,连接BE,由SAS可证BDCEAB,得EA=BD,点B到直线EA的距离是3,根据三角形的面积公式,即可求解.
(1)∵当AC=AB时,△OAB与△OAC是偏差三角形,A(3,2),B(4,0),
∴点C的坐标为(2,0),如图1,
∵AC=AB,
∴∠ACB=∠ABC,
∵∠OCA+∠ACB=180°,
∴∠OBA+∠OCA=180°,
故答案为:(2,0),∠OBA+∠OCA=180°;
(2)△ABC与△ACD是偏差三角形,理由如下:
如图2中,在AD上取一点H,使得AH=AB.
∵AC平分∠BAD,
∴∠CAH=∠CAB,
又∵ AC=AC,
∴△CAH≌△CAB(SAS),
∴CH=CB,∠B=∠AHC,
∵∠B+∠D=180°,∠AHC+∠CHD=180°,
∴∠D=∠CHD,
∴CH=CD,
∴CB=CD,
∵△ACD和△ABC中,AC=AC,∠CAD=∠CAB,BC=CD,△ADC与△ABC不全等,
∴△ABC与△ACD是偏差三角形;
(3)如图3中, 延长CA至点E,使AE=BD,连接BE,
∵∠BAC+∠BDC=180°,∠BAC+∠BAE=180°,
∴∠BDC=∠BAE,
又∵AB=CD,
∴BDCEAB(SAS),
∴EA=BD,
∵点C到直线BD的距离是3,
∴点B到直线EA的距离是3,
∴S△ABC+S△BCD=S△ABC+S△EAB= S△BCE=![]() (AC+EA)×3 =
(AC+EA)×3 =![]() (AC+BD)×3 =
(AC+BD)×3 =![]() ×9×3=
×9×3=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE、CE 分别是∠ABC 和∠ACB 的平分线,过点 E 作 DF∥BC,交 AB 于 D,交 AC 于 F,若 AB=5,AC=4,则△ADF周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年9月第22号台风“山竹”给某地造成严重影响.蓝天救援队驾着冲锋舟沿一条东西方向的河流营救灾民,早晨从![]() 地出发,晚上最后到达
地出发,晚上最后到达![]() 地,约定向东为正方向,当天航行依次记录如下(单位:千米):11,-6,15,-7,18,-8,10,-5,问:
地,约定向东为正方向,当天航行依次记录如下(单位:千米):11,-6,15,-7,18,-8,10,-5,问:
(1)![]() 地在
地在![]() 地的东面,还是西面?与
地的东面,还是西面?与![]() 地相距多少千米?
地相距多少千米?
(2)冲锋舟离开出发地最远是多少千米?
(3)若冲锋舟每千米耗油0.5升,油箱容量为30升,求途中至少需要补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
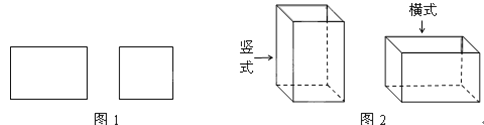
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方形纸箱(加工时接缝材料不计).
若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸盒、横式纸盆各加工多少个,恰好能将购进的纸板全部用完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输公司派出大小两种型号共20辆渣土运输车运输士方.已知一辆大型渣土运输车和两辆小型渣土运输车每次共运20吨;3辆大型渣土运输车和8辆小型渣土运输车每次共运70吨.并且一辆大型渣土运输车运输花费500元/次,一辆小型渣土运输车运输花费300元/次.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)若每次运输主方总不小于148吨,且小型渣土运输车至少派出7辆,问该渣土运输公司有哪几种派出方案?最少需要花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
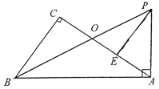
(1)求证:AP=AO;
(2)求证:PE⊥AO.
查看答案和解析>>
科目:初中数学 来源: 题型:
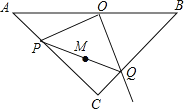
【题目】如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数![]() 的图象上,且x1<x2<x3,( )
的图象上,且x1<x2<x3,( )
A. 若![]() <
<![]() <
<![]() ,则
,则![]() +
+![]() +
+![]() >0B. 若
>0B. 若![]() <
<![]() <
<![]() ,则
,则![]()
![]()
![]() <0
<0
C. 若![]() <
<![]() <
<![]() ,则
,则![]() +
+![]() +
+![]() >0D. 若
>0D. 若![]() <
<![]() <
<![]() ,则
,则![]()
![]()
![]() <0
<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com