
【题目】某运输公司派出大小两种型号共20辆渣土运输车运输士方.已知一辆大型渣土运输车和两辆小型渣土运输车每次共运20吨;3辆大型渣土运输车和8辆小型渣土运输车每次共运70吨.并且一辆大型渣土运输车运输花费500元/次,一辆小型渣土运输车运输花费300元/次.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)若每次运输主方总不小于148吨,且小型渣土运输车至少派出7辆,问该渣土运输公司有哪几种派出方案?最少需要花费多少元?
【答案】(1)一辆大型渣土运输车每次运土方10吨,一辆小型渣土运输车每次运土方5吨;(2)见解析
【解析】
(1)设一辆大型渣土运输车每次运土方x吨,一辆小型渣土运输车每次运土方y吨,根据等量关系,列出二元一次方程组,即可求解;
(2)设小型渣土运输车派出m辆,则大型渣土运输车派出(20-m)辆,根据题意,列出关于m的不等式组,求出m的范围,再取整数,即可得到结论.
(1)设一辆大型渣土运输车每次运土方x吨,一辆小型渣土运输车每次运土方y吨,
依题意,得:![]() ,解得:
,解得:![]() .
.
答:一辆大型渣土运输车每次运土方10吨,一辆小型渣土运输车每次运土方5吨;
(2)设小型渣土运输车派出m辆,则大型渣土运输车派出(20-m)辆,
依题意,得: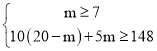 ,
,
解得:7≤m≤10.4,
∵m为整数,
∴m=7,8,9,10.
∴该渣土运输公司有4种排出方案,方案1:派出大型渣土运输车13辆,小型渣土运输车7辆;方案2:派出大型渣土运输车12辆,小型渣土运输车8辆;方案3:派出大型渣土运输车11辆,小型渣土运输车9辆;方案4:派出大型渣土运输车10辆,小型渣土运输车10辆.
方案1所需总费用为500×13+300×7=8600(元);
方案2所需总费用为500×12+300×8=8400(元);
方案3所需总费用为500×11+300×9=8200(元);
方案4所需总费用为500×10+300×10=8000(元).
∵8600>8400>8200>8000,
∴派出大型渣土运输车和小型渣土运输车各10辆花费最少,最少花费为8000元.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )
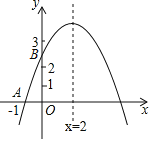
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小泽和小超分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小泽掷得的点数为x,小超掷得的点数为![]() ,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B=__________.
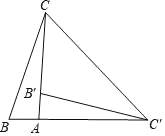
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
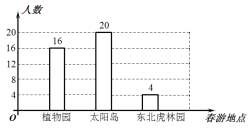
(1)求a的值.
(2)求a名学生中选择去植物园春游的人数占所抽取人数的百分比是多少?
(3)如果该校八年级有440名学生,请你估计选择去太阳岛春游的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个三角形,有两边相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏差三角形.
(1)如图1,已知A(3,2),B(4,0),请在x轴上找一个C,使得△OAB与△OAC是偏差三角形.你找到的C点的坐标是______,直接写出∠OBA和∠OCA的数量关系______.
(2)如图2,在四边形ABCD中,AC平分∠BAD,∠D+∠B=180°,问△ABC与△ACD是偏差三角形吗?请说明理由.
(3)如图3,在四边形ABCD中,AB=DC,AC与BD交于点P,BD+AC=9,∠BAC+∠BDC=180°,其中∠BDC<90°,且点C到直线BD的距离是3,求△ABC与△BCD的面积之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MBC和∠NCB是△ABC的外角,点O是∠MBC和∠NCB的平分线的交点,点O叫做△ABC的旁心.

(1)已知∠A=100°,那么∠BOC等于多少度;
(2)猜想∠BOC与∠A有什么数量关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架直升机从高度为450米的位置开始,先以20米/秒的速度上升60秒,后以12米/秒的速度下降120秒,规定上升为正,下降为负,求:
(1)这时直升机的高度是多少米?
(2)直升机每上升1米耗油![]() 毫升,每下降1米耗油
毫升,每下降1米耗油![]() 毫升(其中
毫升(其中![]() ),问这架直升机在上升和下降的过程中共耗油多少毫升?
),问这架直升机在上升和下降的过程中共耗油多少毫升?
(3)若![]() 是小于
是小于![]() 的最大整数,求(2)问中的值.
的最大整数,求(2)问中的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com