
【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
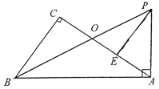
(1)求证:AP=AO;
(2)求证:PE⊥AO.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据等角的余角相等证明即可;
(2)过点O作OD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CO=DO,利用“SAS”证明△APE和△OAD全等,根据全等三角形对应角相等可得∠AEP=∠ADO=90°,从而得证.
(1)证明:∵∠C=90°,∠BAP=90°
∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,
又∵∠CBO=∠ABP,
∴∠BOC=∠APB,
∵∠BOC=∠AOP,
∴∠AOP=∠APB,
∴AP=AO;
(2)证明:如图,过点O作OD⊥AB于D,
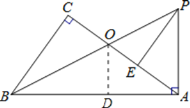
∵∠CBO=∠ABP,
∴CO=DO,
∵AE=OC,
∴AE=OD,
∵∠AOD+∠OAD=90°,∠PAE+∠OAD=90°,
∴∠AOD=∠PAE,
在△AOD和△PAE中,
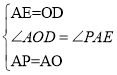 ,
,
∴△AOD≌△PAE(SAS),
∴∠AEP=∠ADO=90°
∴PE⊥AO.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】请把下列证明过程补充完整.已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上,∠1=∠2=∠E,∠3=∠4.求证:AB∥CD.
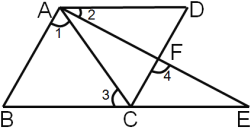
证明:∵∠2=∠E(已知)
∴ ∥BC( )
∴∠3=∠ ( )
∵∠3=∠4(已知)
∴∠4=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF ,即∠BAF=∠
∴∠4=∠ (等量代换)
∴ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
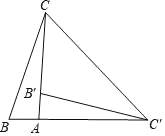
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个三角形,有两边相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏差三角形.
(1)如图1,已知A(3,2),B(4,0),请在x轴上找一个C,使得△OAB与△OAC是偏差三角形.你找到的C点的坐标是______,直接写出∠OBA和∠OCA的数量关系______.
(2)如图2,在四边形ABCD中,AC平分∠BAD,∠D+∠B=180°,问△ABC与△ACD是偏差三角形吗?请说明理由.
(3)如图3,在四边形ABCD中,AB=DC,AC与BD交于点P,BD+AC=9,∠BAC+∠BDC=180°,其中∠BDC<90°,且点C到直线BD的距离是3,求△ABC与△BCD的面积之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MBC和∠NCB是△ABC的外角,点O是∠MBC和∠NCB的平分线的交点,点O叫做△ABC的旁心.

(1)已知∠A=100°,那么∠BOC等于多少度;
(2)猜想∠BOC与∠A有什么数量关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.其中正确结论的个数为

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
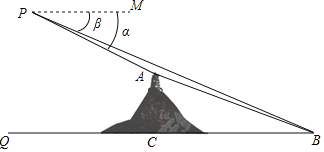
【题目】数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离.如图,无人机所在位置P与岚光阁阁顶A、湖心亭B在同一铅垂面内,P与B的垂直距离为300米,A与B的垂直距离为150米,在P处测得A、B两点的俯角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)
﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内折叠铺平,恰好拼成一个无缝隙无重叠的矩形EFGH,若EH=5,EF=12,则矩形ABCD的面积是( )
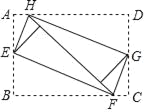
A. 13 B. ![]() C. 60 D. 120
C. 60 D. 120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com