
،¾جâؤ؟،؟2018ؤê9شآµع22؛إج¨·ç،°ة½ضٌ،±¸ّؤ³µطشى³ةردضطس°دى£®ہ¶جى¾بش®¶س¼ف×إ³ه·وضغرطز»جُ¶«خ÷·½دٍµؤ؛سء÷سھ¾بشضأٌ£¬شç³؟´س![]() µط³ِ·¢£¬حيةد×î؛َµ½´ï
µط³ِ·¢£¬حيةد×î؛َµ½´ï![]() µط£¬ش¼¶¨دٍ¶«خھص·½دٍ£¬µ±جى؛½ذذزہ´خ¼اآ¼بçدآ£¨µ¥خ»£؛ا§أ×£©£؛11£¬-6£¬15£¬-7£¬18£¬-8£¬10£¬-5£¬خت£؛
µط£¬ش¼¶¨دٍ¶«خھص·½دٍ£¬µ±جى؛½ذذزہ´خ¼اآ¼بçدآ£¨µ¥خ»£؛ا§أ×£©£؛11£¬-6£¬15£¬-7£¬18£¬-8£¬10£¬-5£¬خت£؛
£¨1£©![]() µطشع
µطشع![]() µطµؤ¶«أو£¬»¹تاخ÷أو£؟سë
µطµؤ¶«أو£¬»¹تاخ÷أو£؟سë![]() µطدà¾à¶àةظا§أ×£؟
µطدà¾à¶àةظا§أ×£؟
£¨2£©³ه·وضغہë؟ھ³ِ·¢µط×îش¶تا¶àةظا§أ×£؟
£¨3£©بô³ه·وضغأ؟ا§أ×؛ؤسح0.5ة£¬سحدنبفء؟خھ30ة£¬اَح¾ضذضءةظذèزھ²¹³ن¶àةظةسح£؟
،¾´ً°¸،؟£¨1£©![]() µطشع
µطشع![]() µطµؤ¶«أو£¬سë
µطµؤ¶«أو£¬سë![]() µطدà¾à28ا§أ×£»£¨2£©³ه·وضغہë؟ھ³ِ·¢µط×îش¶تا33ا§أ×£»£¨3£©ح¾ضذضءةظذèزھ²¹³ن10ةسح£®
µطدà¾à28ا§أ×£»£¨2£©³ه·وضغہë؟ھ³ِ·¢µط×îش¶تا33ا§أ×£»£¨3£©ح¾ضذضءةظذèزھ²¹³ن10ةسح£®
،¾½âخِ،؟
£¨1£©½«؛½ذذ¼اآ¼µؤ¾àہëدà¼س¼´؟ةµأ³ِ´ً°¸£»
£¨2£©¸ù¾ف؛½ذذ¼اآ¼دآµؤت¾ف£¬زہ´خ¼ئثم³ِأ؟´خ¼اآ¼ت±³ه·وضغ¾àہë³ِ·¢µطµؤ¾àہ룬صز³ِئنضذµؤ×î´َضµ¼´؟ة£»
£¨3£©دب¼ئثم³ِ³ه·وضغذذت»µؤ×ـ¾àہ룬´س¶ّ؟ةµأ³ِ×ـ؛ؤسحء؟£¬شظ¸ù¾فسحدنبفء؟خھ30ة¼´؟ةµأ³ِ´ً°¸£®
£¨1£©![]()
![]()
![]()
![]()
زٍ![]() £¬دٍ¶«خھص·½دٍ
£¬دٍ¶«خھص·½دٍ
¹ت![]() µطشع
µطشع![]() µطµؤ¶«أو£¬سë
µطµؤ¶«أو£¬سë![]() µطدà¾à28ا§أ×£»
µطدà¾à28ا§أ×£»
£¨2£©أ؟´خ¼اآ¼ت±£¬³ه·وضغ¾àہë³ِ·¢µطµؤ¾àہëزہ´خبçدآ£؛
µعز»´خخھ![]()
µع¶´خخھ![]()
µعب´خخھ![]()
µعثؤ´خخھ![]()
µعخه´خخھ![]()
µعءù´خخھ![]()
µعئك´خخھ![]()
µع°ث´خخھ![]()
زٍ´ث£¬³ه·وضغہë؟ھ³ِ·¢µط×îش¶تا33ا§أ×£»
£¨3£©³ه·وضغذذت»µؤ×ـ¾àہëخھ![]()
![]()
![]() £¨ا§أ×£©
£¨ا§أ×£©
³ه·وضغ؛½ذذضذµؤ×ـ؛ؤسحء؟خھ![]() £¨ة£©
£¨ة£©
ح¾ضذضءةظذèزھ²¹³نµؤسحء؟خھ![]() £¨ة£©
£¨ة£©
¹تح¾ضذضءةظذèزھ²¹³ن10ةسح£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟½¨ةèزّذذµؤؤ³´¢ذîش±ذ،صإشع°ىہيزµخٌت±£¬ش¼¶¨´وبëخھص£¬ب،³ِخھ¸؛. 2019ؤê10شآ29بص£¬ثûدب؛َ°ىہيءثئك±تزµخٌ£؛ +2000شھ،¢-800شھ،¢+400شھ،¢-800شھ،¢+1400شھ،¢-1700شھ،¢-200شھ.
£¨1£©بôثûشçةدءىب،±¸سأ½ً4000شھ£¬ؤاأ´دآ°àت±س¦½»»طزّذذ_________شھا®.
£¨2£©اëإذ¶دشعصâئك´خ°ىہيزµخٌضذ£¬ذ،صإشعµع_______´خزµخٌ°ىہي؛َتضضذدض½ً×î¶à£¬µع_________´خزµخٌ°ىہي؛َتضضذدض½ً×îةظ.
£¨3£©بôأ؟°ىز»¼زµخٌ£¬زّذذ·¢¸ّزµخٌء؟µؤ0.2%×÷خھ½±ہّ£¬ذ،صإصâجىس¦µأ½±½ً¶àةظشھ?
£¨4£©بô¼اذ،صإµعز»´خ°ىہيزµخٌا°µؤدض½ًخھ0µم£¬سأصغدكح³¼ئح¼±يت¾صâ7´خزµخٌ°ىہيضذذ،صإتضضذدض½ًµؤ±ن»¯اé؟ِ.
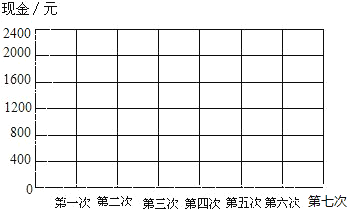
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟اë°ردآءذض¤أ÷¹³ج²¹³نحêصû.زرضھ:بçح¼£¬B،¢C،¢Eبµمشعح¬ز»ض±دكةد£¬A،¢F،¢Eبµمشعح¬ز»ض±دكةد£¬،د1=،د2=،دE£¬،د3=،د4.اَض¤:AB،خCD.
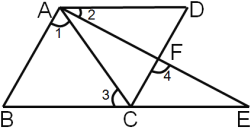
ض¤أ÷:،ك،د2=،دE(زرضھ)
،à ،خBC( )
،à،د3=،د ( )
،ك،د3=،د4(زرضھ)
،à،د4=،د ( )
،ك،د1=،د2(زرضھ)
،à،د1+،دCAF=،د2+،دCAF £¬¼´،دBAF=،د
،à،د4=،د (µبء؟´ْ»»)
،à ( )
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھدآءذ½لآغ£؛¢ظبô![]() £¬شٍ
£¬شٍ![]() »¥خھدà·´ت£»¢عبô
»¥خھدà·´ت£»¢عبô![]() £¬شٍ
£¬شٍ![]() از
از![]() £»¢غ
£»¢غ![]() £»¢ـ¾ّ¶شضµذ،سع10µؤثùسذصûتض®؛حµبسع0£»¢ف3سë-5تاح¬ہàدئنضذصب·µؤ½لآغسذ£¨ £©¸ِ£®
£»¢ـ¾ّ¶شضµذ،سع10µؤثùسذصûتض®؛حµبسع0£»¢ف3سë-5تاح¬ہàدئنضذصب·µؤ½لآغسذ£¨ £©¸ِ£®
A.2B.3C.4D.5
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ذ،شَ؛حذ،³¬·ض±ًسأضہA،¢Bء½أ¶÷»×سµؤ·½·¨ہ´ب·¶¨P(x,y)µؤخ»ضأ£¬ثأا¹و¶¨£؛ذ،شَضہµأµؤµمتخھx£¬ذ،³¬ضہµأµؤµمتخھ![]() ,ؤاأ´£¬ثأا¸÷ضہز»´خثùب·¶¨µؤµمآنشعزرضھض±دكy=-2x+6ةدµؤ¸إآتخھ£¨،،،،£©
,ؤاأ´£¬ثأا¸÷ضہز»´خثùب·¶¨µؤµمآنشعزرضھض±دكy=-2x+6ةدµؤ¸إآتخھ£¨،،،،£©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شع،÷ABCضذ£¬،دAOB=125،م£¬°ر،÷ABC¼ô³ةب²؟·ض£¬±كAB،¢BCAC·إشعح¬ز»ض±دكةد£¬µمO¶¼آنشعض±دكMNةد£¬ازS،÷BCO£؛S،÷CAO£؛S،÷ABO=BC£؛CA£؛AB£¬شٍ،دACBµؤ¶بتخھ£¨،،،،£©
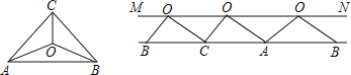
A.70،مB.65،مC.60،مD.85،م
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼,شعRt،÷ABCضذ,،دBAC=90،م,½«،÷ABCبئµمAث³ت±صëذ×ھ90،م؛َµأµ½µؤ،÷AB،نC،ن(µمBµؤ¶شس¦µمتاµمB،ن,µمCµؤ¶شس¦µمتاµمC،ن),ء¬½سCC،ن.بô،دCC،نB،ن=32،م£¬شٍ،دB=__________£®
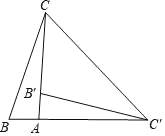
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟¶¨زه£؛بôء½¸ِب½اذخ£¬سذء½±كدàµبازئنضذز»×éµب±كثù¶شµؤ½ا¶شس¦دàµب£¬µ«²»تاب«µبب½اذخ£¬خزأا¾ح³ئصâء½¸ِب½اذخخھئ«²îب½اذخ£®
£¨1£©بçح¼1£¬زرضھA£¨3£¬2£©£¬B£¨4£¬0£©£¬اëشعxضلةدصزز»¸ِC£¬ت¹µأ،÷OABسë،÷OACتائ«²îب½اذخ£®ؤمصزµ½µؤCµمµؤ×ّ±êتا______£¬ض±½سذ´³ِ،دOBA؛ح،دOCAµؤتء؟¹طدµ______£®
£¨2£©بçح¼2£¬شعثؤ±كذخABCDضذ£¬ACئ½·ض،دBAD£¬،دD+،دB=180،م£¬خت،÷ABCسë،÷ACDتائ«²îب½اذخآً£؟اëثµأ÷ہيسة£®
£¨3£©بçح¼3£¬شعثؤ±كذخABCDضذ£¬AB=DC£¬ACسëBD½»سعµمP£¬BD+AC=9£¬،دBAC+،دBDC=180،م£¬ئنضذ،دBDC£¼90،م£¬ازµمCµ½ض±دكBDµؤ¾àہëتا3£¬اَ،÷ABCسë،÷BCDµؤأو»ض®؛ح£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
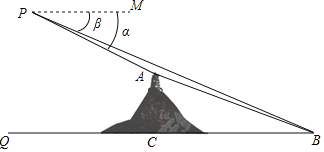
،¾جâؤ؟،؟تر§تµ¼ù»î¶¯ذ،×é½èضْشطسذ²â½ازاµؤخقبث»ْ²âء؟دَة½ل°¹â¸َسëخؤأ÷؛؛ذؤح¤ض®¼نµؤ¾àہ룮بçح¼£¬خقبث»ْثùشعخ»ضأPسëل°¹â¸َ¸َ¶¥A،¢؛ذؤح¤Bشعح¬ز»ا¦´¹أوؤع£¬PسëBµؤ´¹ض±¾àہëخھ300أ×£¬AسëBµؤ´¹ض±¾àہëخھ150أ×£¬شعP´¦²âµأA،¢Bء½µمµؤ¸©½ا·ض±ًخھ¦ء،¢¦آ£¬ازtan¦ء=![]() £¬tan¦آ=
£¬tan¦آ=![]() ©پ1£¬تشاَل°¹â¸َسë؛ذؤح¤ض®¼نµؤ¾àہëAB£®£¨¼ئثم½ل¹ûبô؛¬سذ¸ù؛إ£¬اë±£ءô¸ù؛إ£©
©پ1£¬تشاَل°¹â¸َسë؛ذؤح¤ض®¼نµؤ¾àہëAB£®£¨¼ئثم½ل¹ûبô؛¬سذ¸ù؛إ£¬اë±£ءô¸ù؛إ£©
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com