
����Ŀ��Ϊ�˽����ѧ���μӻ����������ij�ؽ����ֶ�����500������ѧ��ÿ��μӻ�����ʱ����г������飬�������������Ƴ�����ͳ��ͼ�����μӻ�����ʱ���Ϊ���������0.5Сʱ������1Сʱ������1.5Сʱ������2Сʱ����
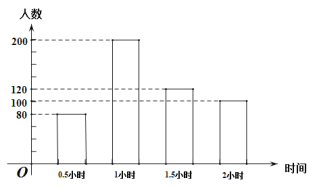
�����ͼʾ���ش��������⣺
��1����ѧ��ÿ�컧��ʱ���ƽ��������������λ����
��2�����ع���12000������ѧ��������Ƹ���ÿ�컧��ʱ�䳬��1Сʱ�ij���ѧ���ж�����?
���𰸡���1��ƽ������1.24��������1����λ����1����2����Уÿ�컧��ʱ�䳬��1Сʱ��ѧ����5280��.
����������1����������ͼ�ɵã�������ʱ��ֱַ�Ϊ��0.5Сʱ������1Сʱ������1.5Сʱ������2Сʱ����������Ȼ�����ƽ��������������λ���Ķ�����;(2)�����500������ÿ�컧��ʱ�䳬��1Сʱ�ij���ѧ����ռ�İٷֱȣ�����12000����.
��1���۲�����ͳ��ͼ����֪�����������ݵ�ƽ�����ǣ�
![]()
�������������ݵ�ƽ������1.24Сʱ��
������1Сʱ
��λ����1Сʱ��
(2)������500��ѧ���У�����ʱ�䳬��1Сʱ����220�ˣ�
���� ![]() ���ˣ�
���ˣ�
���Уÿ�컧��ʱ�䳬��1Сʱ��ѧ����5280��.


 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ�� 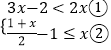 ����������գ���ɱ���Ľ��
����������գ���ɱ���Ľ��
���ⲻ��ʽ�٣���
���ⲻ��ʽ�ڣ���
���Ѳ���ʽ�ٺ͢ڵĽ⼯�������ϱ�ʾ������
������ԭ����ʽ��Ľ⼯Ϊ ![]()
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ֽƬABCD�У�AD=8��AB=6��E�DZ�BC�ϵĵ㣬��ֽƬ��AE�۵���ʹ��B���ڵ�F��������FC������EFCΪֱ��������ʱ��BE�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڣ������̳����д����������һ���Żݹ��│��ע���˿�ֻ��Ϊ�����Ż�ƾ֤���ܶ���������300Ԫ�����ֿ���ƾ����������̳�����۵�8�۹���.
��1���˿������Ԫ������Ʒʱ�����벻��Ǯ��ȣ���ʲô����¹�����㣿
��2��С��Ҫ��һ̨���Ϊ3500Ԫ�ı��䣬��ι�����㣿С���ܽ�ʡ����ԪǮ��
��3��С�Ű�����ķ���������̨�������£�����̳�����ӯ��25������̨����Ľ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
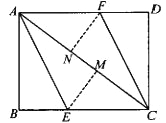
����Ŀ����ͼ��ACΪ����ABCD�ĶԽ��ߣ�����AB��AE�۵���ʹ��B����AC�ϵĵ�M��������CD��CF�۵���ʹ��D����AC�ϵĵ�N����
��1����֤���ı���AECF��ƽ���ı��Σ�
��2����AB=6��AC=10�����ı���AECF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı�����ABCD����EΪAB���ϵ�һ�㣬��FΪ�Խ���BD�ϵ�һ�㣬��EF��AB��
��1�����ı���ABCDΪ�����Σ�
����ͼ1����ֱ��д��AE��DF��������ϵ��
�ڽ���EBF�Ƶ�B��ʱ����ת��ͼ2��ʾ��λ�ã�����AE��DF������AE��DF��������ϵ��˵�����ɣ�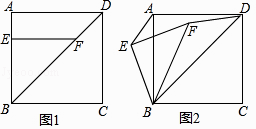
��2����ͼ3�����ı���ABCDΪ���Σ�BC=mAB���������������䣬����EBF�Ƶ�B˳ʱ����ת����0�㣼����90�㣩�õ���E'BF'������AE'��DF'������ͼ3�л�����ͼ����ֱ��д��AE'��DF'��������ϵ��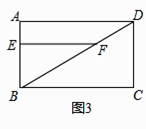
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ӳ���ѵ������Ҫ��Ŀ֮һ������ͼ���е������Ǽס��ҡ�������ÿ��ʮ�ε�����Եijɼ������Թ���Ϊ��������10����ÿ����λ1����1�֣�
�˶�Ա�ײ��Գɼ���
������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ����֣� | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
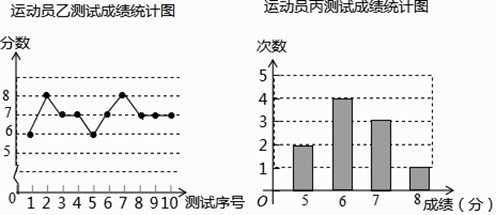
��1��д���˶�Ա�ײ��Գɼ�����������λ����
��2��������������ѡ��һλ����ɼ������ҽ�Ϊ�ȶ��Ľ���������Ϊ�����ˣ�����Ϊѡ˭�����ʣ�Ϊʲô�����ο����ݣ����˳ɼ��ķ���ֱ�ΪS��2=0.8��S��2=0.4��S��2=0.8��
��3���ס��ҡ��������֮����е�����ϰ��ÿ���˵��ȿ��ܵĴ����������ˣ������ȴӼ����д����������ֽ���ʱ��ص������еĸ����Ƕ��٣�������״ͼ���б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒÿ���ɱ�10Ԫ��������ÿ����Ʒ�����ۼ�x��Ԫ�����Ʒ����������y������֮��Ĺ�ϵ���±�
�ۼ�x��Ԫ�� | 15 | 20 | 25 | |
��������y������ | 25 | 20 | 15 |
����������y�����ۼ�x��һ�κ���.
��1�������������y�����������ۼ�x��Ԫ���ĺ�����ϵʽ��
��2�������ۼ۶�Ϊ30Ԫʱ��ÿ�յ���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��4x��m2=0
��1����֤���÷������������ȵ�ʵ����
��2�����÷��̵�����ʵ����x1��x2����x1+2x2=9����m��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com