
分析 设这杯饮料为1,根据题意得第一次后剩下饮料是原来的1-$\frac{1}{2}$=$\frac{1}{2}$,第二次后剩下饮料是原来的1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)=(1-$\frac{1}{2}$)2=$\frac{1}{4}$,第三次后剩下饮料是原来的(1-$\frac{1}{2}$)$\frac{1}{2}$(1-$\frac{1}{2}$)-$\frac{1}{2}$[1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)]=(1-$\frac{1}{2}$)3=$\frac{1}{8}$,由此发现规律,写出第,四次和第n次的结果.
解答 解:设这杯饮料为1,根据题意得
第一次后剩下饮料是原来的:1-$\frac{1}{2}$=$\frac{1}{2}$,
第二次后剩下饮料是原来的:1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)=(1-$\frac{1}{2}$)2=$\frac{1}{4}$,
第三次后剩下饮料是原来的:(1-$\frac{1}{2}$)$\frac{1}{2}$(1-$\frac{1}{2}$)-$\frac{1}{2}$[1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)]=(1-$\frac{1}{2}$)3=$\frac{1}{8}$,
∴第n次后剩下饮料是原来的:(1-$\frac{1}{2}$)n=$\frac{1}{{2}^{n}}$,
故答案为:$\frac{1}{{2}^{n}}$.
点评 本题主要考查数字的变化规律,根据题意分别计算出第一、二、三次剩余的饮料是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图是用相同的正方形砖铺成的地面,一宝物藏在其中某一块砖的下面,则宝物在白色区域的概率是( )
如图是用相同的正方形砖铺成的地面,一宝物藏在其中某一块砖的下面,则宝物在白色区域的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{15}$ | D. | $\frac{8}{15}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2006 | B. | 2014 | C. | 2015 | D. | 2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
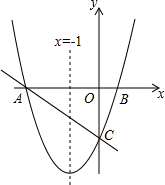 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中点A的坐标为(-3,0),点C为抛物线与y轴的交点.
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中点A的坐标为(-3,0),点C为抛物线与y轴的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com