练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若a、b是关于x的方程x2+x+m=0的两个实数根，则代数式（a-b）2的值为
     
    （用含m的代数式表示）
    考点：根与系数的关系
    专题：
    分析：由若a、b是关于x的方程x2+x+m=0的两个实数根，得出a+b=-1，ab=m，进一步把（a-b）2=（a+b）2-4ab，直接代入求得答案即可．
    解答：解：∵a、b是关于x的方程x2+x+m=0的两个实数根，
    ∴a+b=-1，ab=m，
    ∴（a-b）2=（a+b）2-4ab=1-4m．
    故答案为：1-4m．
    点评：此题考查根与系数的关系：若任意一元二次方程ax2+bx+c=0，有两根X1，X2，则X1+X2=-
    b
    a
    ，X1．X2=
    c
    a
    ．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

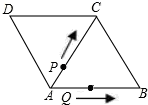    如图，菱形ABCD的边长为12cm，∠B=60°，从初始时刻开始，点P、Q同时从A点出发，点P以2cm/秒的速度沿A→C→B的方向运动，点Q以4cm/秒的速度沿A→B→C→D的方向运动，当Q点运动点D点时，P、Q两点同时停止运动．设P、Q运动的时间为x秒时，解答下列问题：
    （1）点P、Q从出发到相遇所用时间是
     
    秒；
    （2）点P、Q从开始运动到停止的过程中，当△APQ是等边三角形时，请求此时x的值是多少秒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    全面实现低碳生活已逐渐成为人们的共识．某企业为了发展低碳经济，采用技术革新，减少二氧化碳的排放．随着排放量的减少，企业相应获得的利润也有所提高，且相应获得的利润y（万元）与月份x（月）
    （1≤x≤6）的函数关系如图所示：
    （1）根据图象，请判断：y与x（1≤x≤6）的变化规律应该符合
     
    函数关系式；
    （填写序号：①反比例函数、②一次函数、③二次函数）；
    （2）求出y与x（1≤x≤6）的函数关系式（不写取值范围）；
    （3）经统计发现，从6月到8月每月利润的增长率相同，且8月份的利润为151.2万元，求这个增长率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，梯形ABCD中，AD∥BC，∠A=90°，E是AB上一点，EC=ED，∠BEC=75°，∠AED=45°，求证：AB=BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    苹果的进价是每千克1.5元，销售中估计有5%的正常损耗．为避免亏本，商家把售价至少定为
     
    元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知△ABC为等边三角形，AB=3，以C为圆心，1为半径作圆，P为⊙C上一动点，连AP，并绕点A顺时针旋转60°到P′，连接CP′，则CP′的取值范围是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知函数y=x2+mx+2，当1≤x≤2时，y＞0恒成立，则m的取值范围为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    4月27日至29日，国务院总理李克强在重庆实地考察“长江黄金水道”建设．“长江黄金水道”是贯通东、中、西部，通航能力最强的航道，当前“长江黄金水道”干支流的通航里程已经达到96000公里，那么96000用科学记数法可以表示为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：△ABC中，∠ABC=∠ACB，以AB为直径的⊙O交BC于点D．
    （1）如图①，当∠A为锐角时，AC与⊙O交于点E，联结BE，则∠BAC与∠CBE的数量关系是∠BAC=
     
    ∠CBE；
    （2）如图②，若AB不动，AC绕点A逆时针旋转，当∠BAC为钝角时，CA的延长线与⊙O交于点E，联结BE，（1）中∠BAC与∠CBE的数量关系是否依然成立？若成立，请加以证明；若不成立，请说明理由．

    查看答案和解析>>

    同步练习册答案