
 如图,梯形ABCD中,AD∥BC,∠A=90°,E是AB上一点,EC=ED,∠BEC=75°,∠AED=45°,求证:AB=BC.
如图,梯形ABCD中,AD∥BC,∠A=90°,E是AB上一点,EC=ED,∠BEC=75°,∠AED=45°,求证:AB=BC.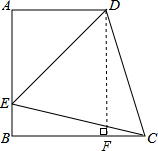 ,
,
|


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
|
|
| 1 |
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
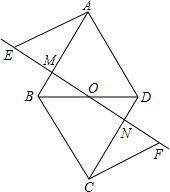 如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形.
如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:
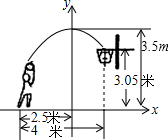 如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米.
如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为
如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com