
【题目】将一块正方形和一块等腰直角三角形如图1摆放.
(1)如果把图1中的△BCN绕点B逆时针旋转90°,得到图2,则∠GBM= ;
(2)将△BEF绕点B旋转.
①当M,N分别在AD,CD上(不与A,D,C重合)时,线段AM,MN,NC之间有一个不变的相等关系式,请你写出这个关系式: ;(不用证明)
②当点M在AD的延长线上,点N在DC的延长线时(如图3),①中的关系式是否仍然成立?若成立,写出你的结论,并说明理由;若不成立,写出你认为成立的结论,并说明理由.
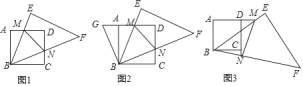
【答案】(1) 45°;(2) ①见解析; ②见解析.
【解析】
(1)由旋转的性质得∠GBA=∠CBN,于是得到∠ABM+∠GBA=45°,即可得到结论;
(2)①根据旋转的性质得到∠GAB=∠C=90°,AG=CN,BG=BN,∠ABG=∠CBN,得到D,A,G三点共线,根据全等三角形的性质得到GM=MN,于是得到结论;
②在AM上截取AG,使得AG=CN,连结BG;根据正方形的性质得到AB=BC,∠A=∠BCN=90°,根据全等三角形的性质得到BG=BN,∠ABG=∠NBC,根据全等三角形的性质即可得到结论.
(1)在正方形ABCD和等腰直角△BEF中,
∵∠ABC=90°,
∴∠EBF=45°,
∴∠ABM+∠CBN=45°,
由旋转的性质得∠GBA=∠CBN,
∴∠ABM+∠GBA=45°,
即∠GBM=45°,
故答案为:45°;
(2)①AM+NC=MN;
理由:∵把图1中的△BCN绕点B逆时针旋转90°得到△ABG,
∴∠GAB=∠C=90°,AG=CN,BG=BN,∠ABG=∠CBN,
∴∠GAB+∠DAB=180°,
∴D,A,G三点共线,
∴∠ABM+∠GBA=45°,
∴∠GBM=∠MBN,
在△GBM与△NBM中,
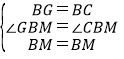 ,
,
∴△GBM≌△NBM,
∴GM=MN,
∵GM=AG+AM=CN+AM,
∴MN=AM+CN;
故答案为:MN=AM+CN;
②上面的式子不成立,结论是:AM﹣NC=MN,
理由:在AM上截取AG,使得AG=CN,连结BG;
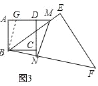
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠BCN=90°,
在△BAG与△BCN中,
 ,
,
∴△BAG≌△BCN,
∴BG=BN,∠ABG=∠NBC,
∴∠MBN=∠MBC+∠CBN=∠MBC+∠ABG=45°=∠GBM,
在△BGM与△BMN中,
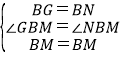
∴△BGM≌△BNM,
∴GM=NM,
∴AM﹣CN=MN.


科目:初中数学 来源: 题型:
【题目】某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.平均修建每公顷大棚要用的支架、塑料膜等材料的费用为![]() 元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为
元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为![]() .每公顷大棚的年平均经济收益为
.每公顷大棚的年平均经济收益为![]() 元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为
元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为![]() 元.
元.
![]() 一年中这个村修建了多少公顷蔬菜大棚?
一年中这个村修建了多少公顷蔬菜大棚?
![]() 若要使收益达到最大,请问应修建多少公顷大棚?并说明理由.
若要使收益达到最大,请问应修建多少公顷大棚?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过240度的部分的电价为每度0.6元;
第二档:月用电量超过240度但不超过400度部分的电价为每度0.65元;
第三档:月用电量超过400度的部分的电价为每度0.9元.
(1)已知老王家去年5月份的用电量为380度,则老王家5月份应交电费 元;
(2)若去年6月份老王家用电的平均电价为0.70元,求老王家去年6月份的用电量;
(3)已知老王家去年7、8月份的用电量共500度(7月份的用电量少于8月份的用电量),两个月的总电价是303元,求老王家7、8月的用电量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
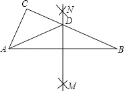
A. 20 B. 22 C. 14 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=8, BC=4,将长方形的一角沿AC折叠,则重叠阴影部分△AFC的面积为( )

A. 14B. 12C.10D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别用标有数字0、﹣1、4的三张卡片(除了数字不同以外,其余都相同)做游戏,他们将卡片洗匀后,将标有数字的一面朝下放在桌面上,甲先随机抽取一张,抽出的卡片放回,乙再从三张卡片中随机抽取一张.若规定甲同学抽到卡片上的数字比乙同学抽取到卡片上的数字大,则甲同学获胜;否则乙同学获胜.请你用列表法或画树状图法求哪名同学获胜的概率大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠C=90°,AC=8cm,BC=6cm,M 在 AC上,且AM=6cm,过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC,若动点 P 从点 A 出发,沿射线 AN 匀速运动,运动速度为 1cm/s,设点 P 运动时间为 t 秒.
(1)经过 秒时,Rt△AMP 是等腰直角三角形?
(2)经过几秒时,PM⊥MB?
(3)经过几秒时,PM⊥AB?
(4)当△BMP 是等腰三角形时,直接写出 t 的所有值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 边长为
边长为![]() 的等边三角形
的等边三角形![]() 的顶点
的顶点![]() 分别在边
分别在边![]() ,
,![]() 上当
上当![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在边
随之在边![]() 上运动,等边三角形的形状保持不变,运动过程中,点
上运动,等边三角形的形状保持不变,运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com