
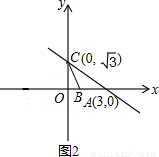
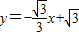 交x轴于点A,交y轴于点C,点B在坐标轴上,△ABC为等腰三角形,且底角等于30°,则点B的坐标为 .
交x轴于点A,交y轴于点C,点B在坐标轴上,△ABC为等腰三角形,且底角等于30°,则点B的坐标为 . 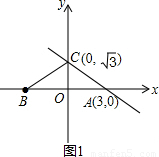 解:∵直线
解:∵直线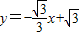 交x轴于点A,交y轴于点C,
交x轴于点A,交y轴于点C,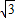 ),
),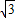 ,OA=3,
,OA=3,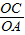 =
=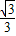 ,
,
 )2=(3-a)2,解得a=1,
)2=(3-a)2,解得a=1,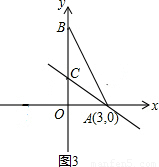
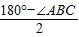 =
=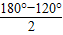 =30°,
=30°, )2=32+(
)2=32+(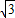 )2,解得y=3
)2,解得y=3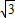 ,
,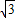 ).
).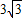 );(1,0).
);(1,0).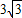 );(1,0).
);(1,0).

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
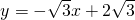 交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.
交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.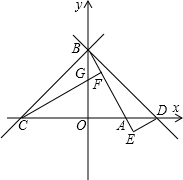
 上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.
上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.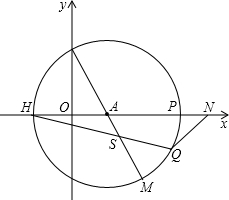
查看答案和解析>>
科目:初中数学 来源:2008-2009学年湖北省武汉市江岸区九年级(上)月考数学试卷(12月份 全册内容)(解析版) 题型:解答题
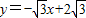 交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.
交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.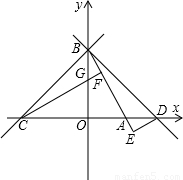
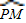 上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.
上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com