Question

如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线 m，垂足分别为点D、E．证明：DE=BD+CE．

（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=120°．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试证明FD=FE．

Answer 1

       证明：（1）∵BD⊥DE，CE⊥DE，

∴∠BDA=∠CEA=90°，

∵∠BAC=90°，

∴∠BAD+∠CAE=∠BAD+∠ABD=90°，

∴∠ABD=∠CAE，

在△ABD和△CAE中，

，

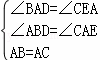∴△ABD≌△CAE（AAS），

∴BD=AE，CE=DA，

∴DE=AE+DA=BD+CE；

（2）DE=BD+CE成立．

理由：∵∠BDA=∠BAC=90°，

∴∠DBA+∠DAB=∠CAE+∠DAB=60°，

∴∠DBA=∠CAE．

在△BAD和△ACE中

，

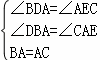∴△ADB≌△CEA（AAS），

∴AE=BD，AD=CE

∴DE=AE+AD=BD+CE；

（3）△DEF为等边三角形

理由：∵△ABF和△ACF均为等边三角形

∴BF=AF=AB=AC=CF，∠BAF=∠CAF=∠ABF=60°，

∴∠BDA=∠AEC=∠BAC=120°，

∴∠DBA+∠DAB=∠CAE+∠DAB=60°，

∴∠DBA=∠CAE．

在△BAD和△ACE中

，

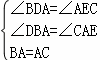∴△ADB≌△CEA（AAS），

∴BD=AE，∠DBA=∠CAE．

∵∠ABF=∠CAF=60°，

∴∠DBA+∠ABF=∠CAE+∠CAF，

∴∠DBF=∠FAE．

在△BDF和△AEF中

，

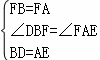∴△DBF≌△EAF（SAS）

∴DF=EF．