
【题目】某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
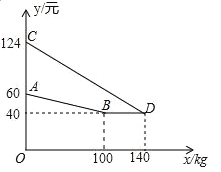
(1)请解释图中点D的实际意义.
(2)求线段CD所表示的y2与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
【答案】(1)点D的横坐标、纵坐标的实际意义:当产量为140kg时,该产品每千克生产成本与销售价相等,都为40元
(2)y2与x之间的函数表达式为y2=﹣![]() x+124(0≤x≤140)
x+124(0≤x≤140)
(3)当该产品的质量为80kg时,获得的利润最大,最大利润为2560元
【解析】
试题分析:(1)点D的横坐标、纵坐标的实际意义:当产量为140kg时,该产品每千克生产成本与销售价相等,都为40元;
(2)根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可;
(3)先求出销售价y2与产量x之间的函数关系,利用:总利润=每千克利润×产量列出有关x的二次函数,求得最值即可.
试题解析:(1)点D的实际意义:当产量为140kg时,该产品每千克生产成本与销售价相等,都为40元.
(2)设线段CD所表示的y2与x之间的函数表达式为y2=k1x+b1,
∵点(0,124),(140,40)在函数y2=k1x+b1的图象上
∴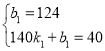 ,解得:
,解得: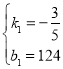 ,
,
∴y2与x之间的函数表达式为y2=﹣![]() x+124(0≤x≤140);
x+124(0≤x≤140);
(3)设线段AB所表示的y1与x之间的函数表达式为y1=k2x+b2,
∵点(0,60),(100,40)在函数y1=k2x+b2的图象上
∴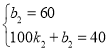 ,解得:
,解得: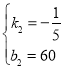 ,
,
∴y1与x之间的函数表达式为y1=﹣![]() x+60(0≤x≤100)
x+60(0≤x≤100)
设产量为x千克时,获得的利润为W元
①当0≤x≤100时,W=[(﹣![]() x+124)﹣(﹣
x+124)﹣(﹣![]() x+60)]x=﹣
x+60)]x=﹣![]() (x﹣80)2+2560,
(x﹣80)2+2560,
∴当x=80时,W的值最大,最大值为2560元.
②当100≤x≤140时,W=[(﹣![]() x+124)﹣40]x=﹣
x+124)﹣40]x=﹣![]() (x﹣70)2+2940
(x﹣70)2+2940
由﹣![]() <0知,当x≥70时,W随x的增大而减小
<0知,当x≥70时,W随x的增大而减小
∴当x=100时,W的值最大,最大值为2400元.
∵2560>2400,
∴当该产品的质量为80kg时,获得的利润最大,最大利润为2560元.


科目:初中数学 来源: 题型:
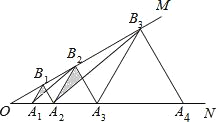
【题目】如图,已知∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,分别连接A1B2,连接A2B3….若OA1=a,从左往右的阴影面积依次记作S1、S2、S3…Sn.则Sn= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线x=![]() .
.

(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合采用全面调查(普查)方式的是( )
A. 对漓江水质情况的调查. B. 对端午节期间市场上粽子质量情况的调查.
C. 对某班50名同学体重情况的调查. D. 对某类烟花爆竹燃放安全情况的调查.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com