
 ��ͼ��A��B��ֱ��l�ϵ����㣬AB=4���ף���l��һ��C��CD��l������BC��l����ɵ����Ϊ60�㣬�߶�BC=2���ף�����P��Q�ֱ��B��Cͬʱ������P��1����/����ٶȣ�����B��C�ķ����˶���Q��2����/����ٶȣ�����C��D�ķ����˶�����P��Q�˶���ʱ��Ϊt�룬��t��2ʱ��PA��CD�ڵ�E��
��ͼ��A��B��ֱ��l�ϵ����㣬AB=4���ף���l��һ��C��CD��l������BC��l����ɵ����Ϊ60�㣬�߶�BC=2���ף�����P��Q�ֱ��B��Cͬʱ������P��1����/����ٶȣ�����B��C�ķ����˶���Q��2����/����ٶȣ�����C��D�ķ����˶�����P��Q�˶���ʱ��Ϊt�룬��t��2ʱ��PA��CD�ڵ�E������ ��1����������ó�BP=t��CQ=2t��PC=t-2���ٸ���EC��AB���ó�$\frac{EC}{AB}$=$\frac{PC}{PB}$�����ó�EC��ֵ�����ɱ�ʾ��CE��QE�ij���
��2����QEΪ�ױߣ���P��l�Ĵ������ߣ�����P���ٶȿ�����t��ʾ��BP��Ҳ������BP�͡�1�����Һ�������ߣ���ô�ؼ�����QE�ij������ǿ��Ը���Q���ٶ���ʱ��t��ʾ��CQ����ôֻҪ���CE���ɣ������������εĶ�Ӧ�߶γɱ�������CE�ij�������������PEC��������PAB���ƣ��ɵó�����CE��AB��PC��BC�ı���ʽ����BP��BC��AB��ֵ�������ú�t��ʽ�ӱ�ʾ��CE��Ҳ�ͱ�ʾ����QE����ô�ɸ��������ε������ʽ���ó�����S��t�ĺ�����ϵʽ��
��3�����QEǡ��ƽ��������APQ���������ô��ʱP��CD��CD��l֮��ľ������ȣ���ôC����PB���е㣬�ɸ���BP=2BC���t��ֵ��Ȼ����ݣ�1���еó��ı�ʾQE��ʽ�ӣ���t���뼴�ɵó�QE��ֵ���ɣ�
��� �⣺��1��������֪��BP=t��CQ=2t��PC=t-2��
��EC��AB��
��$\frac{EC}{AB}$=$\frac{PC}{PB}$��
��EC=$\frac{PC•AB}{PB}$=$\frac{4��t-2��}{t}$��
��QE=QC-EC=2t-$\frac{4��t-2��}{t}$=$\frac{2��{t}^{2}-2t+4��}{t}$��
��2����ͼ����PF��L��F����DC�ӳ�����M��AN��CD��N��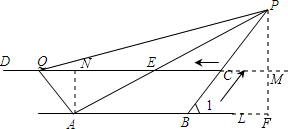
�ڡ�PBF�У�PF=PB•sin60��=$\frac{\sqrt{3}}{2}$t��
��S��APQ=S��AQE+S��PQE
=$\frac{1}{2}$QE•AN+$\frac{1}{2}$QE•PM=$\frac{1}{2}$QE•PF
=$\frac{1}{2}$��$\frac{2��{t}^{2}-2t+4��}{t}$��$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{2}$��t2-2t+4����
��3����ʱ��EΪPA���е㣬����CҲ��PB���е㣬
��t-2=2��
��t=4��
��QE=$\frac{2��{t}^{2}-2t+4��}{t}$=$\frac{2��{4}^{2}-2��4+4��}{4}$=6�����ף���
���� ���������������ۺ��⣬��Ҫ���������������ε������Լ���ֱ�������ε�Ӧ�õ�֪ʶ�㣬�������������ε����ʵó���ʾCE��ʽ���ǽ���Ĺؼ����ڣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
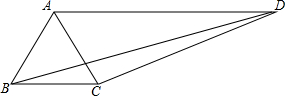 ���ı���ABCD�У����ӶԽ���AC��BD��AB=BC��DC=6��AD=9���ҡ�ABC=2��ADC=60�㣬��BD=3$\sqrt{13}$��
���ı���ABCD�У����ӶԽ���AC��BD��AB=BC��DC=6��AD=9���ҡ�ABC=2��ADC=60�㣬��BD=3$\sqrt{13}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
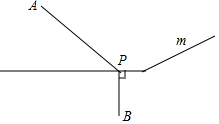 ��ͼ��ʾ����������ׯA��B�����ĺ������Խ��Ƶؿ���һ�����߶Σ�ͼ��m��A��B�ֱ��ںӵ����ԣ���Ҫ�ںӱ���һ��ˮ��վ��ͬʱ��A��B���幩ˮ��Ϊ�˽�Լ����ķ��ã���Ҫʹ������Ĺܵ���̣�ij�˼�����������Ľ��飺�ӵ�B��ӵ������߽�m�ڵ�P�����PΪˮ��վ��λ�ã�
��ͼ��ʾ����������ׯA��B�����ĺ������Խ��Ƶؿ���һ�����߶Σ�ͼ��m��A��B�ֱ��ںӵ����ԣ���Ҫ�ںӱ���һ��ˮ��վ��ͬʱ��A��B���幩ˮ��Ϊ�˽�Լ����ķ��ã���Ҫʹ������Ĺܵ���̣�ij�˼�����������Ľ��飺�ӵ�B��ӵ������߽�m�ڵ�P�����PΪˮ��վ��λ�ã��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
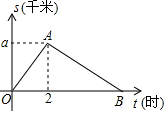 ƽ��ɽ�н����־���'���߳���·���������ij��ʦ������������ؽ���·������̬������ԭ·���أ��ý�ʦ�뿪����·��S��ǧ�ף��벽��ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�����д���㵽����̬��ƽ���ٶ���4ǧ��/Сʱ����2Сʱ������ͼ���ṩ��Ϣ�������������
ƽ��ɽ�н����־���'���߳���·���������ij��ʦ������������ؽ���·������̬������ԭ·���أ��ý�ʦ�뿪����·��S��ǧ�ף��벽��ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�����д���㵽����̬��ƽ���ٶ���4ǧ��/Сʱ����2Сʱ������ͼ���ṩ��Ϣ��������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
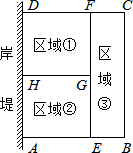 Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ��İ��̣������㹻����Ϊһ�ߣ����ܳ�Ϊ80��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ���������������������������������ȣ���BC�ij���Ϊx�ף���������ABCD�����Ϊy��2��
Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ��İ��̣������㹻����Ϊһ�ߣ����ܳ�Ϊ80��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ���������������������������������ȣ���BC�ij���Ϊx�ף���������ABCD�����Ϊy��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
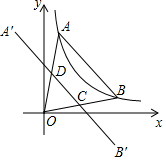 ��ͼ����A��B�ں���y=$\frac{1}{x}$��x��0����ͼ���ϣ���A�ڵ�B����࣬��OA=OB����A����y��ĶԳƵ�ΪA�䣬��B����x��ĶԳƵ�ΪB�䣬����A��B��ֱ�OA��OB�ڵ�D��C�����ı���ABCD�����Ϊ$\frac{6}{5}$�����A������Ϊ��$\frac{1}{2}$��2������C������Ϊ��$\frac{6}{5}$��$\frac{3}{10}$����
��ͼ����A��B�ں���y=$\frac{1}{x}$��x��0����ͼ���ϣ���A�ڵ�B����࣬��OA=OB����A����y��ĶԳƵ�ΪA�䣬��B����x��ĶԳƵ�ΪB�䣬����A��B��ֱ�OA��OB�ڵ�D��C�����ı���ABCD�����Ϊ$\frac{6}{5}$�����A������Ϊ��$\frac{1}{2}$��2������C������Ϊ��$\frac{6}{5}$��$\frac{3}{10}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com