解:(1)
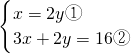
,
把①代入②,得3×2y+2y=16,
解得:y=2,
把y=2代入①,得x=4,
∴原方程组的解为

;
(2)
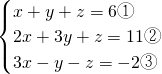
①+③得:4x=4,
解得:x=1,
②+③,得5x+2y=9④,
把x=1代入④,得y=2,
把x=1,y=2代入①,得z=3,
∴原方程组的解为
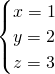
.
分析:(1)将第一个方程代入第二个方程中消去x求出y的值,进而求出x的值,即可确定出原方程组的解;
(2)第一个方程与第三个方程相加消去y与z求出x的值,第二个方程与第三个方程相加消去z得到关于x与y的方程,将x的值代入求出y的值,将x,y的值代入第一个方程求出z的值,即可确定出原方程组的解.
点评:此题考查了解二元一次方程组,以及解三元一次方程组,利用了消元的思想,消元的方法有两种:加减消元法与代入消元法.

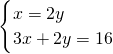
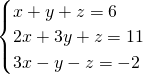 .
.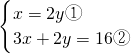 ,
, ;
;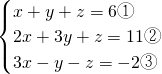
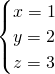 .
.

 名校课堂系列答案
名校课堂系列答案