
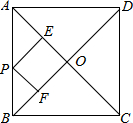
 如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5.
如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=5. 分析 连接PO,由AC=10可求得AO=OB=5,利用S△APO+S△BPO=S△ABO,可求得PE+PF.
解答 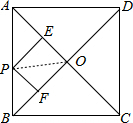 解:如图,连接PO,
解:如图,连接PO,
∵四边形ABCD为正方形,
∴AO=OB=$\frac{1}{2}$AC=5,且AO⊥BO,
∴S△AOB=$\frac{1}{2}$AO•BO=$\frac{1}{2}$×5×5=$\frac{25}{2}$,
∵PE⊥AC,PF⊥BD,
∴S△APO=$\frac{1}{2}$AO•PE=$\frac{5}{2}$PE,S△BPO=$\frac{1}{2}$BO•PF=$\frac{5}{2}$PF,
又S△APO+S△BPO=S△ABO,
∴$\frac{5}{2}$PE+$\frac{5}{2}$PF=$\frac{25}{2}$,
∴PE+PF=5,
故答案为:5.
点评 本题主要考查正方形的性质,掌握正方形的四边相等、对角线相等垂直且平分是解题的关键,注意等积法的运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
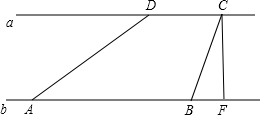 如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com