
分析 (1)首先确定A和C的坐标,利用待定系数法即可求得函数的解析式;
(2)AC与对称轴的交点就是P,首先求得AC的解析式,则P的坐标即可求得;
(3)在y轴的正半轴上截取OH=OD=1,则H的坐标是(0,1),延长DH交AC于点G,则DG⊥AC,∠CDH=∠CDO-∠CAO,当F在x轴的负半轴上时,当∠CFO=∠CDH=∠CDO-∠CAO时,则△CFO∽△CDG,根据相似三角形的对应边的比相等即可求得OF的长,则F的坐标即可求得,然后根据对称性求得F在x轴的正半轴时的坐标;
(4)当抛物线沿y轴的正半轴移动时,Q的横坐标是1,QO平分∠CQN,则CQ=OC,利用勾股定理即可求得Q的纵坐标;同理求得抛物线沿y轴的负半轴移动时Q的坐标.
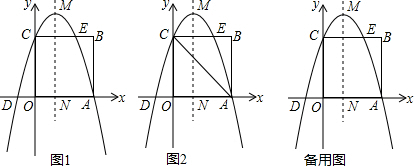
解答 解:(1)∵四边形OABC是正方形,B的坐标是(3,3),
∴A的坐标是(3,0),C的坐标是(0,3).
根据题意得$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
则二次函数的解析式是y=-x2+2x+3;
(2)设直线AC的解析式是y=ax+b,
$\left\{\begin{array}{l}{3a+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$,
则直线AC的解析式是y=-x+3,
当x=1时,y=-1+3=2,
则P的坐标是(1,2);
(3)在y=-x2+2x+3中令y=0,则-x2+2x+3=0,解得x=-1或x=3.
则D的坐标是(-1,0)A的坐标是(3,0).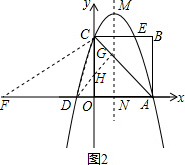
在y轴的正半轴上截取OH=OD=1,则H的坐标是(0,1),延长DH交AC于点G,则DG⊥AC;
∵直角△ODF中,OH=OD,
∴∠HDO=45°,
同理,∠CAO=45°,
∴∠HDO=∠CAO.则∠CDH=∠CDO-∠CAO.
当F在x轴的负半轴上时,
设DG的解析式是y=ex+f,则$\left\{\begin{array}{l}{-e+f=0}\\{f=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{e=1}\\{f=1}\end{array}\right.$,则DG的解析式是y=x+1.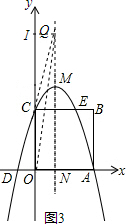
根据题意得:$\left\{\begin{array}{l}{y=-x+3}\\{y=x+1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
则G的坐标是(1,2).
则DG=$\sqrt{(1+1)^{2}+{2}^{2}}$=2$\sqrt{2}$,CD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,CG=$\sqrt{{1}^{2}+(3-2)^{2}}$=$\sqrt{2}$.
当∠CFO=∠CDH=∠CDO-∠CAO时,△CFO∽△CDG,
则$\frac{CG}{CO}=\frac{DG}{OF}$,即$\frac{\sqrt{2}}{3}=\frac{2\sqrt{2}}{OF}$,解得:OF=6,
则F的坐标是(-6,0).
根据对称性可得当F在x轴的正半轴上时F的坐标是(6,0);
(4)当抛物线沿y轴的正半轴移动时,如图3,
设Q的坐标是(1,n).作QI⊥y轴于点I.则IQ=1,IC=n-3,
则QO平分∠CQN,则CQ=OC=3,12+(n-3)2=32,
解得:n=3+2$\sqrt{2}$,
则Q的坐标是(1,3+2$\sqrt{2}$);
同理,当抛物线沿y轴的负方向移动时Q的坐标是(1,3-2$\sqrt{2}$).
总之,Q的坐标是(1,3+2$\sqrt{2}$)或(1,3-2$\sqrt{2}$).
点评 本题是相似三角形,二次函数以及等腰三角形的性质的综合应用,正确作出辅助线,构造相似三角形是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
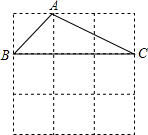 如图,△ABC的三个顶点分别在格子的3个交点上,请你试着再在格子的交点上找出三个点D,E,F,使得△DEF≌△ABC.
如图,△ABC的三个顶点分别在格子的3个交点上,请你试着再在格子的交点上找出三个点D,E,F,使得△DEF≌△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
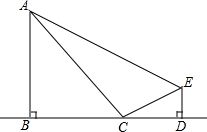 如图,分别过点A、E作AB⊥BD,ED⊥BD,C为线段BD上一动点,连接AC、EC.已知AB=9,DE=1,AE=17,设CD=x,用含x的代数式表示AC+CE.
如图,分别过点A、E作AB⊥BD,ED⊥BD,C为线段BD上一动点,连接AC、EC.已知AB=9,DE=1,AE=17,设CD=x,用含x的代数式表示AC+CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com