
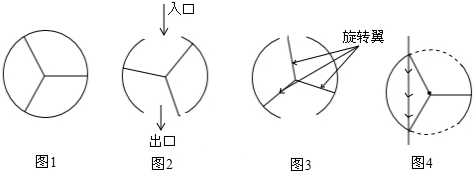
分析 根据旋转的性质和弧长的公式进行分析解答即可.
解答 解:因为旋转门的三片旋转翼组成的角是360°,
所以可得两片旋转翼之间的夹角是$\frac{1}{3}×360°$=120°;
因为旋转翼在圆形空间内旋转,若每分钟转4圈,且门的三个扇形部分最多可容纳2个人,
所以可得:30分钟内,通过的人=4×30×2×3=720;
因为旋转门的圆形周长是6m,
可得:要使空气无法在出入口自由流动,每个门口的最大弧形(虚线部分)的长应为l=$\frac{60×\frac{1}{2}×6}{180}=1$,
故答案为:120;720;1m.
点评 此题考查旋转问题,关键是根据旋转的性质分析,再利用弧长的公式计算.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
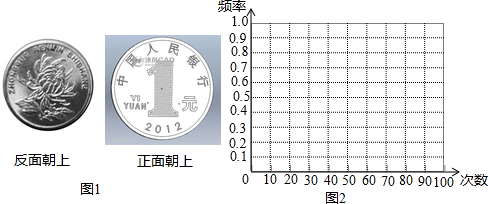
| 实验次数n | 10 | 20 | 30 | 40 | 50 | 60 | 80 | 100 |
| 正面朝上的次数m | 7 | 12 | 15 | 18 | 27 | 27 | 44 | 49 |
| 正面朝上的频率$\frac{m}{n}$ | 0.7 | 0.6 | 0.5 | 0.45 | 0.54 | 0.45 | 0.55 | 0.49 |
| 反面朝上的次数p | 3 | 8 | 15 | 22 | 23 | 33 | 36 | 51 |
| 反面朝上的频率$\frac{p}{n}$ | 0.3 | 0.4 | 0.5 | 0.55 | 0.46 | 0.55 | 0.45 | 0.51 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象经过点(2,2) | B. | y随x的增大而减小 | ||
| C. | 图象位于第一、三象限 | D. | 当x<1时,y的值都大于2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com