
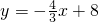 与X轴Y轴分别交于点M,N,如果点P在坐标轴上,以点P为圆心,
与X轴Y轴分别交于点M,N,如果点P在坐标轴上,以点P为圆心, 为半径的圆与直线
为半径的圆与直线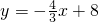 相切,则符合要求的点P个数可能为
相切,则符合要求的点P个数可能为 x+4相切于点A,
x+4相切于点A,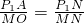
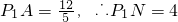 ,
, x+4上切于点B,连接P3B.
x+4上切于点B,连接P3B.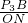 =
=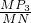 ,
, ,
,

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源:2012年江苏省苏州市吴江市青云中学中考数学二模试卷(解析版) 题型:解答题
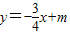 与x轴y轴分别交于点A和点B,点B的坐标为(0,6)
与x轴y轴分别交于点A和点B,点B的坐标为(0,6)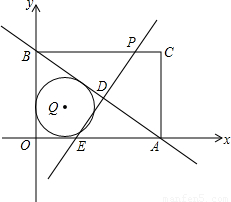
查看答案和解析>>
科目:初中数学 来源:2012年10月中考数学模拟试卷(19)(解析版) 题型:解答题
 与x轴y轴分别交于点A和点B,点B的坐标为(0,6)
与x轴y轴分别交于点A和点B,点B的坐标为(0,6)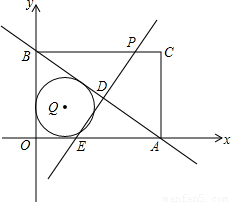
查看答案和解析>>
科目:初中数学 来源:2013年江苏省无锡市江阴市中考数学一模试卷(解析版) 题型:解答题
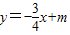 与x轴y轴分别交于点A和点B,点B的坐标为(0,6)
与x轴y轴分别交于点A和点B,点B的坐标为(0,6)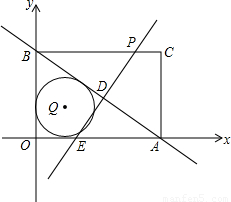
查看答案和解析>>
科目:初中数学 来源:2010年山东省济宁市济宁师专附中中考数学模拟试卷(解析版) 题型:解答题
 与x轴y轴分别交于点M,N,
与x轴y轴分别交于点M,N, 为半径的圆与直线y=-
为半径的圆与直线y=- 相切,求点P的坐标.
相切,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2011年广东省汕头市八年级第十四章《一次函数》单元测试数学卷 题型:解答题
如图,直线 与x轴y轴分别交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0)。(1)求
与x轴y轴分别交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0)。(1)求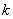 的值;(2)若点P(
的值;(2)若点P(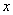 ,
,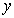 )是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3)探究:当点P运动到什么位置时,△OPA的面积为,并说明理由。
)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3)探究:当点P运动到什么位置时,△OPA的面积为,并说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com