
如图,在Rt△ABC中,∠BAC=90°,∠B=45°,O为BC中点,如果点M、N分别在线段AB、AC上移动,设AM的长为x,CN的长为y,且x、y满足等式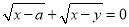 (a>0)
(a>0)

(1)求证:BM=AN;
(2)请你判断△OMN的形状,并证明你的结论;
(3)求证:当OM∥AC时,无论a取何正数,△OMN与△ABC面积的比总是定值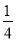 .
.
(1)证明见解析;(2)△OMN是等腰直角三角形,证明见解析;(3)证明见解析.
【解析】
试题分析:(1)由等式可得出x=y=a,结合等腰直角三角形的性质,即可证得;
(2)作OE⊥AC,OF⊥AB,通过证明△OFM≌△OEN,可得OM=ON,根据全等三角形的性质,只要证得∠MON=90°,即可证得;
(3)当OM∥AC时,OM、ON是等腰Rt△ABC的中位线,由三角形的面积计算公式,表示出三角形的面积,比较出其比值即可;
试题解析:(1)∵∠A=90°,∠B=45°,
∴∠C=45°,从而AB=AC;
由等式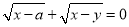 (a>0),知x=y=a,AM=CN=a,
(a>0),知x=y=a,AM=CN=a,
∴BM=AB-AM=AC-CN=AN
(2)△OMN是等腰直角三角形。证明如下:
连AO,
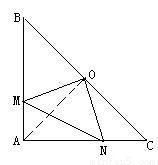
∵AB=AC,O为BC中点,
∴∠BAO=∠CAO=90°÷2=45°且AO⊥BC;
∵∠B=∠C=45°,
∴AO=BO=CO;
又BM=AN,
∴△BMO≌△ANO(SAS),
∴OM=ON,∠BOM=∠AON,
∴∠MON=∠AON+∠MOA=∠BOM+∠MOA=90°,即MO⊥NO,
故△OMN是等腰直角三角形
(3)当OM∥AC时,知∠BOM=∠A=90°,
由于∠B=45°,
∴△BMO是等腰直角三角形,从而∠BOM=45°;
∵∠MON=90°,
∴∠CON=45°,
又∠C=45°,
∴∠ONC=90°,
∵OM=ON,OB=OC,
∴且△BMO和△CNO是全等的等腰直角三角形(HL),
∴BM=MO=NO=NC=a,
由(1)知AN=BM=a,
∴AC=AB=2a,
∴△OMN与△ABC面积的比=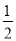 a2:
a2: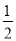 (2a)2=
(2a)2=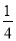 ,
,
故结论成立
考点:1.全等三角形的判定与性质;2.等腰直角三角形.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源:2014-2015学年江苏省东台第一教研片七年级下学期第一次月考数学卷(解析版) 题型:选择题
在下列条件中①∠A+∠B=∠C ②∠A﹕∠B﹕∠C=1﹕2﹕3 ③∠A= ∠B=
∠B=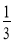 ∠C ④∠A=∠B=2∠C ⑤∠A=∠B=
∠C ④∠A=∠B=2∠C ⑤∠A=∠B= ∠C 中能确定△ABC为直角三角形的条件有( ).
∠C 中能确定△ABC为直角三角形的条件有( ).
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台第一教研片八年级下学期第一次月考数学卷(解析版) 题型:选择题
下列图形中,中心对称图形有( ).

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省衡阳市七年级上学期期末考试数学试卷(解析版) 题型:选择题
计算: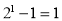 ,
, ,
,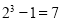 ,
,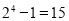 ,
,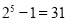 ,·····归纳各计算结果中的个位数字规律,则
,·····归纳各计算结果中的个位数字规律,则 的个位数字是( )。
的个位数字是( )。
A.1 B.3 C.7 D.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省衡阳市八年级上学期期末考试数学试卷(解析版) 题型:填空题
若等腰三角形的顶角为80°,则它腰上的高与底边的夹角为______度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城东台苏东双语九年级上学期第一次质量检测数学试卷(解析版) 题型:解答题
(1)引入:如图1,直线AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC,直线BC是否与⊙O相切,为什么?

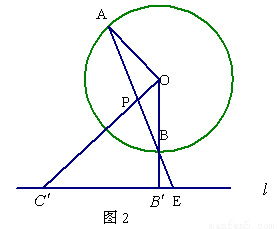
(2)引申:记(1)中⊙O的切线为直线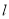 ,在(1)的条件下,如图2,将切线
,在(1)的条件下,如图2,将切线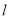 向下平移,设平移后的直线
向下平移,设平移后的直线 与OB的延长线相交于点
与OB的延长线相交于点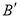 ,与AB的延长线相交于点E,与OP的延长线相交于点
,与AB的延长线相交于点E,与OP的延长线相交于点 .
.
找出图2中与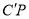 相等的线段,并说明理由;
相等的线段,并说明理由;
如果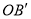 =9cm,
=9cm, =12cm,⊙O的半径为6cm,试求线段
=12cm,⊙O的半径为6cm,试求线段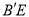 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次模拟数学试卷(解析版) 题型:选择题
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=( )

A.1:16 B. 1:18 C.1:20 D.1:24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com