
如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE′,连接EE′,则EE′的长等于_______.

 .
.
【解析】
试题分析:根据旋转的性质得到: ,在
,在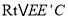 中:EC=DC-DE=2,
中:EC=DC-DE=2, ,根据勾股定理得到
,根据勾股定理得到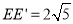 .
.
故答案为: .
.
考点:旋转的性质;勾股定理.
考点分析: 考点1:图形的平移与旋转 定义:

科目:初中数学 来源:2014-2015学年天津市和平区九年级下学期结课质量调查数学试卷(解析版) 题型:选择题
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则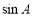 =( )
=( )

(A) (B)
(B)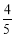 (C)
(C) (D)
(D)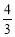
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省枣庄市九年级3月测试数学试卷(解析版) 题型:解答题
(本题6分)如图所示,在⊙O中,  =
=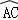 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.

(1)求证:AC2=ABAF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省学业水平模拟考试数学试卷(解析版) 题型:解答题
(本小题满分8分)有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的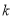 ,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的
,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的 .
.

(1)写出 为负数的概率;
为负数的概率;
(2)求一次函数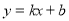 的图象经过二、三、四象限的概率。(用树状图或列表法求解)
的图象经过二、三、四象限的概率。(用树状图或列表法求解)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省学业水平模拟考试数学试卷(解析版) 题型:选择题
如下图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点.连结MP,MQ,PQ,在整个运动过程中,△MPQ的面积大小变化情况是( ).
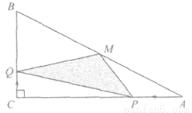
A.一直增大 B.一直减小 C.先减小后增大 D.先增大后减小
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省东港市九年级九校联考数学试卷(解析版) 题型:解答题
(14分)把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
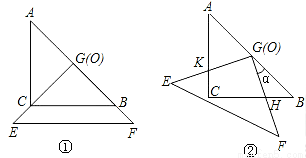
(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;(要有辅助线哟!)
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的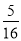 ,若存在,求出此时x值;若不存在,说明理由。
,若存在,求出此时x值;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com