
抛物线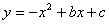 与x轴交与
与x轴交与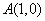 ,
,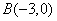 两点,
两点,
(1)求该抛物线的解析式;
(2)设(1)中的抛物线与y轴交于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(1)y=-x2-2x+3;(2)Q(-1,2)
解析试题分析:(1)由题意把A(1,0)B(-3,0)代入到抛物线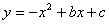 中即可求得结果;
中即可求得结果;
(2)过B、C作直线BC与对称轴x=-1的交点就是Q点,设直线BC解析式为y=kx+b,把B(-3,0)C(0,3)代入得直线BC的解析式,令XQ=-1,得YQ=2,即可求得结果.
(1)把A(1,0)B(-3,0)代入到抛物线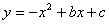 中得
中得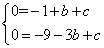 ,解得
,解得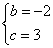
∴抛物线的解析式为y=-x2-2x+3;
(2)存在。
过B、C作直线BC与对称轴x=-1的交点就是Q点,
设直线BC解析式为y=kx+b,把B(-3,0)C(0,3)代入得 ,解得
,解得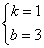
∴y="x+3"
令XQ=-1,得YQ=2
∴Q(-1,2).
考点:二次函数的性质
点评:二次函数的性质是初中数学的重点和难点,是中考常见题,一般难度不大,需熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
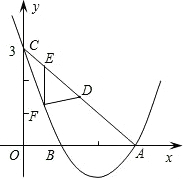 交于点A、B.
交于点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•邯郸一模)已知:如图,抛物线y=-x2+bx+c的图象经过点A(1,0),B (0,5)两点,该抛物线与x轴的另一交点为C.
(2012•邯郸一模)已知:如图,抛物线y=-x2+bx+c的图象经过点A(1,0),B (0,5)两点,该抛物线与x轴的另一交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
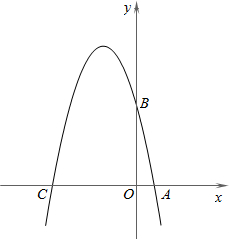 已知:如图,抛物线y=-x2+bx+c的图象经过点A(1,0),B (0,5)两点,该抛物线与x轴的另一交点为C.
已知:如图,抛物线y=-x2+bx+c的图象经过点A(1,0),B (0,5)两点,该抛物线与x轴的另一交点为C.查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(35):2.8 二次函数的应用(解析版) 题型:解答题
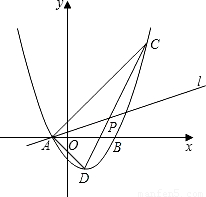
查看答案和解析>>
科目:初中数学 来源:第23章《二次函数与反比例函数》中考题集(32):23.5 二次函数的应用(解析版) 题型:解答题
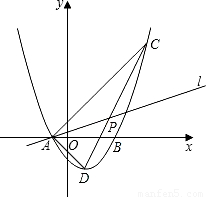
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com