
 如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是$\widehat{AD}$上一点,连结AG,CG.
如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是$\widehat{AD}$上一点,连结AG,CG.分析 (1)结论:∠ACE=∠AGC.首先证明AB垂直平分CD,推出AC=AD,∠ACD=∠ADC,因为∠AGC=∠ADC,由此即可证明.
(2)如图2中,由DG∥AB,推出∠AEC=∠CDG=90°,推出CG是直径,推出∠CAG=90°,由此即可证明.
(3)如图3中,连接OC、BC.只要证明△OBC是等边三角形即可解决问题.
解答 解:(1)结论:∠ACE=∠AGC.理由如下:
如图1中,连接AD.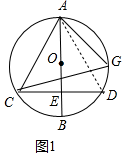
∵AB是直径,AB⊥CD,
∴EC=ED,
∴AD=AC,
∴∠ACE=∠ADC,
∵∠AGC=∠ADC,
∴∠ACE=∠AGC.
(2)证明:如图2中,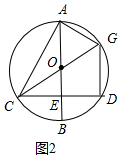
∵DG∥AB,
∴∠AEC=∠CDG=90°,
∴CG是直径,
∴∠CAG=90°,
∵∠CAG=∠AEC=90°,∠AGC=∠ACE,
∴△ACG∽△EAC.
(3)解:如图3中,连接OC、BC.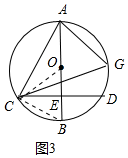
∵OE=EB,CE⊥OB,
∴CO=CB=OB,
∴△OBC是等边三角形,
∴∠B=60°,
∴∠AGC=∠B=60°.
点评 本题考查相似三角形综合题、圆的有关知识、直径的判定和性质、等边三角形的判定和性质、线段的垂直平分线的性质和判定等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线,属于中考压轴题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:解答题
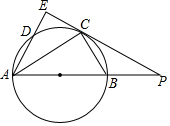 如图,Rt△APE,∠AEP=90°,以AB为直径的⊙,O交PE于C,且AC平分∠EAP.连接BC,PB:PC=1:2.
如图,Rt△APE,∠AEP=90°,以AB为直径的⊙,O交PE于C,且AC平分∠EAP.连接BC,PB:PC=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1题 | B. | 2题 | C. | 3题 | D. | 4题 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象的开口向下 | B. | 当x>1时,y随x的增大而减小 | ||
| C. | 当x<1时,y随x的增大而减小 | D. | 图象的对称轴是直线x=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com