
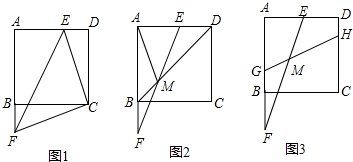
分析 (1)△CEF是等腰直角三角形;证明△FBC≌△EDC即可得出结论,注意不要忽略直角;
(2)过E作EN∥AB,证明△FBM≌△ENM可知FM=EM,则AM是直角△AEF斜边上的中线,要想求AM的长,求斜边EF的长即可,利用勾股定理求EF;
(3)连接EC和FC,证明四边形FCHG是平行四边形,得出FC=GH=3$\sqrt{5}$,利用勾股定理求BF,则就是DE的长.
解答 解:(1)如图1,△CEF是等腰直角三角形,理由是:
在正方形ABCD中,BC=DC,∠FBC=∠D=90°,
∵BF=DE,
∴△FBC≌△EDC,
∴CF=CE,∠ECD=∠FCB,
∴∠ECF=∠ECB+∠FCB=∠ECB+∠ECD=90°,
∴△CEF是等腰直角三角形;
(2)如图2,过E作EN∥AB,交BD于N,则EN=ED=2,
∵BN∥AD ,
,
∴∠F=∠MEN,
∵∠BMN=∠EMN,
∴△FBM≌△ENM,
∴EM=FM,
在Rt△EAF中,EF=$\sqrt{{4}^{2}+(6+2)^{2}}$=4$\sqrt{5}$,
∴AM=$\frac{1}{2}$EF=2$\sqrt{5}$;
(3)如图3,连接EC和FC ,
,
由(1)得∠EFC=45°,
∵∠EMH=45°,
∴∠EFC=∠EMH,
∴GH∥FC,
∵AF∥DC,
∴四边形FCHG是平行四边形,
∴FC=GH=3$\sqrt{5}$,
由勾股定理得:BF=$\sqrt{(3\sqrt{5})^{2}-{6}^{2}}$=3,
∴DE=BF=3.
点评 本题是四边形综合题,考查了正方形和平行四边形、等腰直角三角形的判定和性质,通过作辅助线构建全等三角形得出边相等和角相等,因此本题辅助线的作法是关键;故在几何证明中,恰当的作辅助线可以把四边形的问题转化为三角形的问题,使问题得以解决.


科目:初中数学 来源: 题型:选择题
 如图是小亮跳远时沙坑的示意图,测量成绩时先使皮尺从后脚跟的点A处开始并与起跳线l于点B处成直角,然后记录AB的长度,这样做的理由是( )
如图是小亮跳远时沙坑的示意图,测量成绩时先使皮尺从后脚跟的点A处开始并与起跳线l于点B处成直角,然后记录AB的长度,这样做的理由是( )| A. | 垂线段最短 | B. | 过两点有且只有一条直线 | ||
| C. | 两点之间线段最短 | D. | 过一点可以做无数条直线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
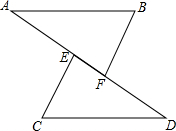 如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.
如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省成都市金堂县八年级上学期期末考试数学试卷就(解析版) 题型:解答题
2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度. 小军为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.
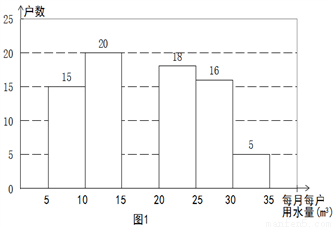
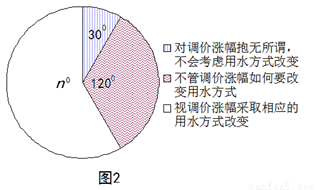
小军发现每月每户的用水量在5m3-35m3之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变. 根据小军绘制的图表和发现的信息,完成下列问题:
(1)n =________,小明调查了_____户居民,并补全图1;
(2)每月每户用水量的中位数落在______之间,众数落在_______之间;
(3)如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com