
【题目】如图,将两块三角板的顶点重合.
(1)请写出图中所有以![]() 点为顶点且小于平角的角;
点为顶点且小于平角的角;
(2)你写出的角中相等的角有________;
(3)若![]() ,试求
,试求![]() 的度数;
的度数;
(4)当三角板![]() 绕点
绕点![]() 适当旋转(保持两三角板有重合部分)时,
适当旋转(保持两三角板有重合部分)时,![]() 与
与![]() 之间具有怎样的数量关系?
之间具有怎样的数量关系?

【答案】(1)见解析;(2) ∠AOC=∠DOB,∠AOD=∠COB; (3) 127°;(4)见解析.
【解析】
(1)根据角的定义写出即可;(2)根据等腰直角三角形AOC和直角三角形DOB,求出相等的角后,写出即可;(3)求出∠AOD,代入∠AOB=∠AOD+∠DOB求出即可;(4)求出∠AOD,代入∠AOB=∠AOD+∠DOB求出即可.
(1)图中所有以O点为顶点且小于平角的角有∠AOD,∠AOC,∠AOB,∠DOC,∠DOB,∠COB.
(2)图中相等的角有∠AOC=∠DOB,∠AOD=∠COB,
故答案为:∠AOC=∠DOB,∠AOD=∠COB.
(3)∵∠DOC=53°,∠AOC=90°,
∴∠AOD=90°-53°=37°,
∵∠DOB=90°,
∴∠AOB=∠AOD+∠DOB=90°+37°=127°.
(4)∠AOB=180°-∠DOC,
理由是:∵∠AOC=90°,
∴∠AOD=90°-∠DOC,
∵∠DOB=90°,
∴∠AOB=∠AOD+∠DOB.
=90°-∠DOC+90°
=180°-∠DOC,
即∠AOB=180°-∠DOC.


科目:初中数学 来源: 题型:
【题目】(背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究. (操作)如图,在矩形ABCD中,AD=6,AB=4,点P是BC边上一点,现将△APB沿AP对折,得△APM,显然点M位置随P点位置变化而发生改变
(问题)试求下列几种情况下:点M到直线CD的距离
(1)∠APB=75°;
(2)P与C重合;
(3)P是BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动。设该机器人每秒前进或后退1步,并且每步的距离为一个单位长度,![]() 表示第n秒时机器人在数轴上位置所对应的数。则下列结论中正确的有______.(只需填入正确的序号)
表示第n秒时机器人在数轴上位置所对应的数。则下列结论中正确的有______.(只需填入正确的序号)
①![]() ②
②![]() ③
③![]() ④
④![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=300,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是( )

A. ②④ B. ①③ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( ) 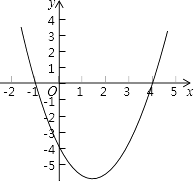
A.无解
B.x=1
C.x=﹣4
D.x=﹣1或x=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.

(1)求证:四边形ADCF是平行四边形;
(2)当AB与AC有何数量关系时,四边形ADCF为矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y= ![]() 的图象过点A(1,2).
的图象过点A(1,2). 
(1)求该函数的解析式;
(2)过点A分别向x轴和y轴作垂线,垂足为B和C,求四边形ABOC的面积;
(3)求证:过此函数图象上任意一点分别向x轴和y轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
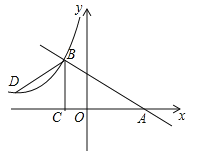
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com