
分析 (1)根据题意得出各式之间变化规律进而得出答案;
(2)首先找出有理化因式进而化简求出答案;
(3)直接将各式化简进而求出答案.
解答 解:(1)①$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1;
②$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$-$\sqrt{2}$;
③$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\sqrt{4}$-$\sqrt{3}$;…
第n个等式:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(2)$\frac{1}{2\sqrt{3}+\sqrt{11}}$=$\frac{\sqrt{12}-\sqrt{11}}{(\sqrt{12}+\sqrt{11})(\sqrt{12}-\sqrt{11})}$=$\sqrt{12}$-$\sqrt{11}$=2$\sqrt{3}$-$\sqrt{11}$;
(3)$\frac{1}{{1+\sqrt{2}}}+\frac{1}{{\sqrt{2}+\sqrt{3}}}+\frac{1}{{\sqrt{3}+2}}+…+\frac{1}{{\sqrt{2014}+\sqrt{2015}}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{3}$-2+…+$\sqrt{2015}$-$\sqrt{2014}$
=-1+$\sqrt{2015}$.
点评 此题主要考查了分母有理化,正确化简二次根式是解题关键.


科目:初中数学 来源: 题型:填空题
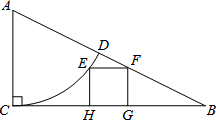 如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4.
如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.
已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,将△ABC折叠,使点B恰好落
如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,将△ABC折叠,使点B恰好落查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{3}x$ | B. | $\frac{4}{3}xy$ | C. | $-\frac{4}{3}x$ | D. | $-\frac{4}{3}x{y^{10}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com