
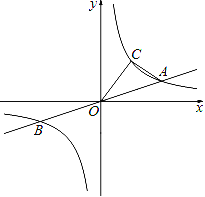
【题目】已知:如图,直线y=![]() x与双曲线
x与双曲线![]() 交于A、B两点,且点A的坐标为(6,m).
交于A、B两点,且点A的坐标为(6,m).
(1)求双曲线![]() 的解析式;
的解析式;
(2)点C(n,4)在双曲线![]() 上,求△AOC的面积;
上,求△AOC的面积;
(3)在(2)的条件下,在x轴上找出一点P,使△AOC的面积等于△AOP的面积的三倍.请直接写出所有符合条件的点P的坐标.
【答案】(1)y=![]() ;(2)9;(3) P(3,0)或P(﹣3,0)
;(2)9;(3) P(3,0)或P(﹣3,0)
【解析】试题分析:(1)、首先根据一次函数的解析式得出点A的坐标,然后根据点A的坐标得出反比例函数的解析式;(2)、作CD⊥x轴于D点,AE⊥x轴于E点,根据题意得出点C的坐标,然后根据S△AOC=S四边形COEA﹣S△AOE=S四边形COEA﹣S△COD=S梯形CDEA得出答案;(3)、设P点坐标为(x,0)根据△AOP的面积求出x的值,从而得出点P的坐标.
试题解析:解:(1)∵点A(6,m)在直线y=![]() x上, ∴m=
x上, ∴m=![]() ×6=2,
×6=2,
∵点A(6,2)在双曲线![]() 上, ∴
上, ∴![]() ,解得k=12,
,解得k=12,
∴双曲线的解析式为y=![]() ;
;
(2)作CD⊥x轴于D点,AE⊥x轴于E点,如图, ∵点C(n,4)在双曲线![]() 上,
上,
∴![]() ,解得n=3,即点C的坐标为(3,4), ∵点A,C都在双曲线
,解得n=3,即点C的坐标为(3,4), ∵点A,C都在双曲线![]() 上,
上,
∴S△OCD=S△AOE=![]() ×12=6, ∴S△AOC=S四边形COEA﹣S△AOE=S四边形COEA﹣S△COD=S梯形CDEA,
×12=6, ∴S△AOC=S四边形COEA﹣S△AOE=S四边形COEA﹣S△COD=S梯形CDEA,
∴S△AOC=![]() (CD+AE)DE=
(CD+AE)DE=![]() (4+2)×(6﹣3)=9;
(4+2)×(6﹣3)=9;
(3)∵S△AOC=9, ∴S△AOP=3,
设P点坐标为(x,0),而A点坐标为(6,2),
∴S△AOP=![]() ×2×|x|=3,解得x=±3,
×2×|x|=3,解得x=±3,
∴P(3,0)或P(﹣3,0).


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……
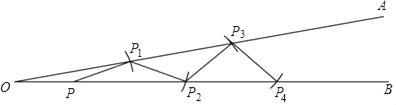
请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批自行车. 男式自行车价格为![]() 元/辆,女式自行车价格为
元/辆,女式自行车价格为![]() 元/辆,要求男式自行车比女式单车多
元/辆,要求男式自行车比女式单车多![]() 辆,设购进女式自行车
辆,设购进女式自行车![]() 辆,购置总费用为
辆,购置总费用为![]() 元.
元.
(1)求购置总费用![]() (元)与女式单车
(元)与女式单车![]() (辆)之间的函数关系式;
(辆)之间的函数关系式;
(2)若两种自行车至少需要购置![]() 辆,且购置两种自行车的费用不超过
辆,且购置两种自行车的费用不超过![]() 元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-4,3),点B(-4,0),OA=5,以点O为直角顶点,点C在第一象限内,作等腰直角△AOC.
(1)直接写出点C坐标:
(2)直接写出四边形ABOC的面积:
(3)在y轴找一点P,使得△BOP的面积等于四边形ABOC的面积,请直接写出点P坐标:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)正方形ABCD,E、F分别在边BC、CD上(不与端点重合),∠EAF=45°,EF与AC交于点G
①如图(i),若AC平分∠EAF,直接写出线段EF,BE,DF之间等量关系;
②如图(ⅱ),若AC不平分∠EAF,①中线段EF,BE,DF之间等量关系还成立吗?若成立请证明;若不成立请说明理由
(2)如图(ⅲ),矩形ABCD,AB=4,AD=8.点M、N分别在边CD、BC上,AN=2![]() ,∠MAN=45°,求AM的长度.
,∠MAN=45°,求AM的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在一个长方形广场的四角都设计一块半径相同的四分之一圆形的花坛.若广场的长为m米,宽为n米,圆形的半径为r米.
(1)列式表示广场空地的面积.
(2)若广场的长为300米,宽为200米,圆形的半径为30米,求广场空地的面积(计算结果保留π).
(3)如图2所示,在(2)的条件下,若在广场的中间再建一个半径为R的圆形花坛,使广场的空地面积不少于广场总面积的![]() ,求R的最大整数值(π取3.1).
,求R的最大整数值(π取3.1).
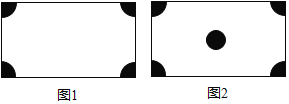
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店出售A、B两种商品,一月份这两种商品的利润都是10万元,后因某种原因确定增加出售A种商品的数量,使A种商品每月利润的增长率都为a,同时减少B种商品的数量,使B种商品每月利润减少的百分率也都是a,(1)分别求出二月份出售A和B两种商品的利润是多少万元?(2)求出三月份出售A、B两种商品的总利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣2x+c(a≠0)与x轴、y轴分别交于点A,B,C三点,已知点A(﹣2,0),点C(0,﹣8),点D是抛物线的顶点.
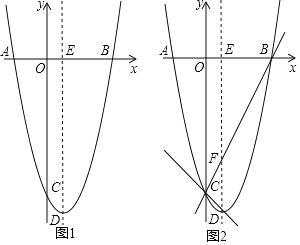
(1)求抛物线的解析式及顶点D的坐标;
(2)如图1,抛物线的对称轴与x轴交于点E,第四象限的抛物线上有一点P,将△EBP沿直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,求点P的坐标;
(3)如图2,设BC交抛物线的对称轴于点F,作直线CD,点M是直线CD上的动点,点N是平面内一点,当以点B,F,M,N为顶点的四边形是菱形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com