
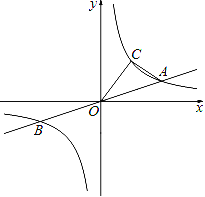
【题目】在平面直角坐标系中,已知点A(-4,3),点B(-4,0),OA=5,以点O为直角顶点,点C在第一象限内,作等腰直角△AOC.
(1)直接写出点C坐标:
(2)直接写出四边形ABOC的面积:
(3)在y轴找一点P,使得△BOP的面积等于四边形ABOC的面积,请直接写出点P坐标:

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
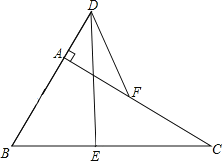
【题目】如图,在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使2AD=AB.连接DE,DF.
(1)求证:AF与DE互相平分;
(2)若BC=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
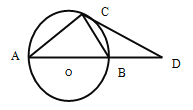
【题目】已知:如图,AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和图形,写出三个正确的结论(AO=BO=BD除外)________;_____________;____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
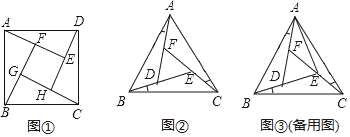
【题目】【问题背景】
如图①所示,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
【类比研究】
如图②所示,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)连结AE,若AF=DF,AB=7,求△DEF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=![]() x与双曲线
x与双曲线![]() 交于A、B两点,且点A的坐标为(6,m).
交于A、B两点,且点A的坐标为(6,m).
(1)求双曲线![]() 的解析式;
的解析式;
(2)点C(n,4)在双曲线![]() 上,求△AOC的面积;
上,求△AOC的面积;
(3)在(2)的条件下,在x轴上找出一点P,使△AOC的面积等于△AOP的面积的三倍.请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
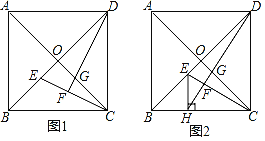
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2017年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车?
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知A型车的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆.根据销售经验,A型车不少于B型车的2倍,但不超过B型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com