
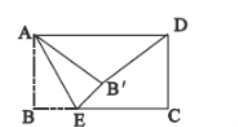
【题目】如图,![]() 是矩形
是矩形![]() 的边
的边![]() 上一点,以
上一点,以![]() 为折痕翻折,使得点
为折痕翻折,使得点![]() 的对应点落在矩形内部点
的对应点落在矩形内部点![]() 处,连接
处,连接![]() ,若
,若![]() ,
,![]() ,当
,当![]() 是以
是以![]() 为底的等腰三角形时,
为底的等腰三角形时,![]() ___________.
___________.
【答案】![]()
【解析】
过点B'作B'F⊥AD,延长FB'交BC与点G,可证四边形ABGF是矩形,AF=BG=4,∠BGF=90°,由勾股定理可求B'F=3,可得B'G=2,由勾股定理可求BE的长.
解:如图,过点B'作B'F⊥AD,延长FB'交BC与点G,
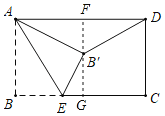
∵四边形ABCD是矩形
∴AD=BC=8,∠DAB=∠ABC=90°
∵AB'=B'D,B'F⊥AD
∴AF=FD=4,
∵∠DAB=∠ABC=90°,B'F⊥AD
∴四边形ABGF是矩形
∴AF=BG=4,∠BGF=90°
∵将△ABE以AE为折痕翻折,
∴BE=B'E,AB=AB'=5
在Rt△AB'F中,![]()
∴B'G=2
在Rt△B'EG中,B'E2=EG2+B'G2,
∴BE2=(4-BE)2+4
∴BE=![]()
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】桐城市发起了“保护龙眠河”行动,某学校七年级两个班的115名学生积极参与,踊跃捐款,已知甲班有![]() 的学生每人捐了10元,乙班有
的学生每人捐了10元,乙班有![]() 的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人。
的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人。
(1)用含x的代数式表示乙班人数: ;
(2)用含x的代数式表示两班捐款的总额;
(3)若x=60,则两班共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……
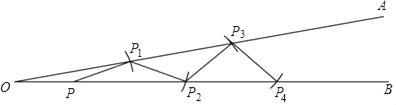
请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2-4x+3的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求点A,点B和点D的坐标;
(2)在y轴上是否存在一点P,使PBC为等腰三角形?若存在,请求出点P的坐标;
(3)若动点M从点A出发,以每秒1个单位长度的速度沿AB向点B运动,同时另一个动点N从点D出发,以每秒2个单位长度的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,MNB的面积最大,试求出最大面积.

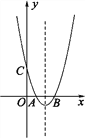 (备用图)
(备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
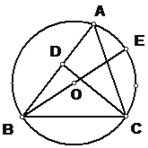
【题目】已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC·BC=BE·CD;
(2)已知CD=6、AD=3、BD=8,求⊙O的直径BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批自行车. 男式自行车价格为![]() 元/辆,女式自行车价格为
元/辆,女式自行车价格为![]() 元/辆,要求男式自行车比女式单车多
元/辆,要求男式自行车比女式单车多![]() 辆,设购进女式自行车
辆,设购进女式自行车![]() 辆,购置总费用为
辆,购置总费用为![]() 元.
元.
(1)求购置总费用![]() (元)与女式单车
(元)与女式单车![]() (辆)之间的函数关系式;
(辆)之间的函数关系式;
(2)若两种自行车至少需要购置![]() 辆,且购置两种自行车的费用不超过
辆,且购置两种自行车的费用不超过![]() 元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-4,3),点B(-4,0),OA=5,以点O为直角顶点,点C在第一象限内,作等腰直角△AOC.
(1)直接写出点C坐标:
(2)直接写出四边形ABOC的面积:
(3)在y轴找一点P,使得△BOP的面积等于四边形ABOC的面积,请直接写出点P坐标:

查看答案和解析>>
科目:初中数学 来源: 题型:
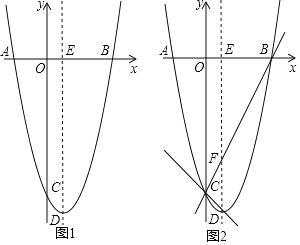
【题目】如图,抛物线y=ax2﹣2x+c(a≠0)与x轴、y轴分别交于点A,B,C三点,已知点A(﹣2,0),点C(0,﹣8),点D是抛物线的顶点.
(1)求抛物线的解析式及顶点D的坐标;
(2)如图1,抛物线的对称轴与x轴交于点E,第四象限的抛物线上有一点P,将△EBP沿直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,求点P的坐标;
(3)如图2,设BC交抛物线的对称轴于点F,作直线CD,点M是直线CD上的动点,点N是平面内一点,当以点B,F,M,N为顶点的四边形是菱形时,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com