
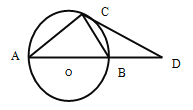
【题目】已知:如图,AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和图形,写出三个正确的结论(AO=BO=BD除外)________;_____________;____________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】线段AB=20cm,M是线段AB的中点,C是线段AB的延长线上的点,AC=3BC,D是线段BA的延长线上的点,且DB=AC.
![]()
(1)求线段BC,DC的长;
(2)试说明M是线段DC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
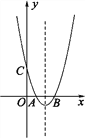
【题目】如图,二次函数y=x2-4x+3的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求点A,点B和点D的坐标;
(2)在y轴上是否存在一点P,使PBC为等腰三角形?若存在,请求出点P的坐标;
(3)若动点M从点A出发,以每秒1个单位长度的速度沿AB向点B运动,同时另一个动点N从点D出发,以每秒2个单位长度的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,MNB的面积最大,试求出最大面积.

 (备用图)
(备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
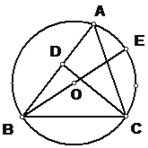
【题目】已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC·BC=BE·CD;
(2)已知CD=6、AD=3、BD=8,求⊙O的直径BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批自行车. 男式自行车价格为![]() 元/辆,女式自行车价格为
元/辆,女式自行车价格为![]() 元/辆,要求男式自行车比女式单车多
元/辆,要求男式自行车比女式单车多![]() 辆,设购进女式自行车
辆,设购进女式自行车![]() 辆,购置总费用为
辆,购置总费用为![]() 元.
元.
(1)求购置总费用![]() (元)与女式单车
(元)与女式单车![]() (辆)之间的函数关系式;
(辆)之间的函数关系式;
(2)若两种自行车至少需要购置![]() 辆,且购置两种自行车的费用不超过
辆,且购置两种自行车的费用不超过![]() 元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
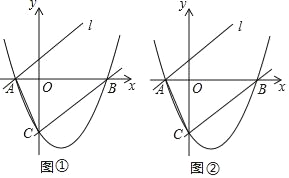
【题目】如图所示,抛物线y=![]() ﹣
﹣![]() x﹣4与x轴交于点A、B,与y 轴相交于点C.
x﹣4与x轴交于点A、B,与y 轴相交于点C.
(1)求直线BC的解析式;
(2)将直线BC向上平移后经过点A得到直线l:y=mx+n,点D在直线l上,若以A、B、C、D为顶点的四边形是平行四边形,求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-4,3),点B(-4,0),OA=5,以点O为直角顶点,点C在第一象限内,作等腰直角△AOC.
(1)直接写出点C坐标:
(2)直接写出四边形ABOC的面积:
(3)在y轴找一点P,使得△BOP的面积等于四边形ABOC的面积,请直接写出点P坐标:

查看答案和解析>>
科目:初中数学 来源: 题型:
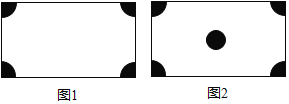
【题目】如图1所示,在一个长方形广场的四角都设计一块半径相同的四分之一圆形的花坛.若广场的长为m米,宽为n米,圆形的半径为r米.
(1)列式表示广场空地的面积.
(2)若广场的长为300米,宽为200米,圆形的半径为30米,求广场空地的面积(计算结果保留π).
(3)如图2所示,在(2)的条件下,若在广场的中间再建一个半径为R的圆形花坛,使广场的空地面积不少于广场总面积的![]() ,求R的最大整数值(π取3.1).
,求R的最大整数值(π取3.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和直线CD相交于点O,OF平分∠COE,过点O作OG⊥OF.

(1)若∠AOE=80°,∠COF=22°,则∠BOD= ;
(2)若∠COE=40°,试说明:OG平分∠DOE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com