
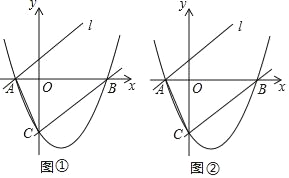
【题目】如图所示,抛物线y=![]() ﹣
﹣![]() x﹣4与x轴交于点A、B,与y 轴相交于点C.
x﹣4与x轴交于点A、B,与y 轴相交于点C.
(1)求直线BC的解析式;
(2)将直线BC向上平移后经过点A得到直线l:y=mx+n,点D在直线l上,若以A、B、C、D为顶点的四边形是平行四边形,求出点D的坐标.
【答案】(1)直线的解析式为y=![]() x﹣4;(2)点D的坐标为(4,4)或(﹣8,﹣4).
x﹣4;(2)点D的坐标为(4,4)或(﹣8,﹣4).
【解析】分析:(1)根据自变量与函数值得对应关系,可得A,B,C的坐标,根据待定系数法,可得答案;
(2)根据平行线的关系,可得m的值,根据待定系数法,可得n的值,根据勾股定理,可得AD,根据平行线的性质,可得关于x的方程,根据解方程,可得x值,再根据自变量与函数值得对应关系,可得D点坐标.
详解:(1)令y=0,得![]() x2-
x2-![]() x-4=0,
x-4=0,
解得:x1=-2,x2=6,
则得点A(-2,0),点B(6,0);
令x=0,得y=-4,
得点C(0,-4).
设直线BC的解析式为y=kx+b,由题意得:
![]() ,
,
解得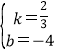 ,
,
∴直线的解析式为y=![]() x-4;
x-4;
(2)由将直线BC向上平移后经过点A得到直线:y=mx+n,
∴m=![]() ,
,
即y=![]() x+n,则
x+n,则![]() ×(-2)+n=0,
×(-2)+n=0,
∴n=![]() ,
,
则直线的解析式为:y=![]() x+
x+![]() ,
,
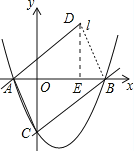
若以A、B、C、D为顶点的四边形是平行四边形,又AD∥BC,
∴AD=BC.
∵点在直线l上,设点D的坐标为(x,![]() x+
x+![]() ),过点D作DE⊥AB于E,
),过点D作DE⊥AB于E,
则AE2+DE2=AD2,又AD=BC![]() ,
,
∴(x+2)2+(![]() x+
x+![]() )2=52,
)2=52,
解得:x1=4,x2=-8.
当x=4时,![]() x+
x+![]() =4;
=4;
当x=-8时,![]() x+
x+![]() =-4,
=-4,
故点D的坐标为(4,4)或(-8,-4).


科目:初中数学 来源: 题型:
【题目】甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )
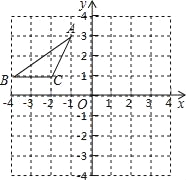
A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1) C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
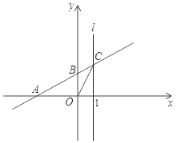
【题目】如图,已知点A(﹣3,0),点B(0,m),直线l:x=1.直线AB与直线l交于点C,连结OC.
(1)△OBC的面积与△OAC的面积比是否是定值?如果是,请求出面积比;如果不是,请说明理由.
(2)若m=2,点T在直线l上且TA=TB,求点T的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
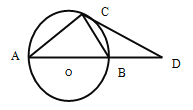
【题目】已知:如图,AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和图形,写出三个正确的结论(AO=BO=BD除外)________;_____________;____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长春市市政工程中需要铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时,每天铺设管道的长度比原计划增加10%,结果提前6天完成,求实际每天铺设管道的长度与实际施工天数.某同学根据题意列出方程![]() ,则方程中未知数x所表示的量是( )
,则方程中未知数x所表示的量是( )
A. 原计划每天铺设管道的长度 B. 实际每天铺设管道的长度
C. 原计划施工的天数 D. 实际施工的天数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ADB=60°,∠CDB=50°.
(1)若AD∥BC,AB∥CD,求∠ABC的度数;
(2)若∠A=70°,请写出图中平行的线段,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() .
.
(1)请以AB、BC为邻边用两种不同的方法画平行四边形ABCD,并说明此画法的合理性(不写作法,保留作图痕迹.);
(2)在上述画出的平行四边形中,若![]() ,
,![]() ,
,![]() ,求对角线BD的长.
,求对角线BD的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com