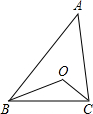
解:(1)∠BOC=

∠A+90°.
∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∵BO,CO分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠BOC+

∠ABC+

∠ACB=180°,
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC=

∠A+90°;
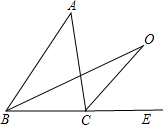
(2)∠BOC=

∠A.
∵∠A+∠ABC=∠ACE.
∵∠OBC+∠BOC=∠OCE,
∵BO,CO分别是∠ABC和∠ACE的平分线,
∵∠ABC=2∠OBC,∠ACE=2∠OCE,
由以上各式可推得∠BOC=

∠A.
分析:根据“三角形的外角等于与其不相邻的两内角和”和角平分线性质.
(1)先列出∠A、∠ABC、∠ACB的关系,再列出∠BOC、∠OBC、∠OCB的关系,然后列出∠ABC和∠OBC、∠ACB和∠OCB的关系;
(2)列出∠A、∠ABC、∠ACE的关系,再列出∠OBC、∠O、∠OCE的关系,然后列出∠ABC和∠OBC、∠ACE和∠OCE的关系.
点评:本题涉及角平分线及三角形的内角和定理等知识,难度一般.

 ∠A+90°.
∠A+90°. ∠ABC+
∠ABC+ ∠ACB=180°,
∠ACB=180°, ∠A+90°;
∠A+90°; ∠A.
∠A. ∠A.
∠A.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案 =2,∠ADC=30°
=2,∠ADC=30°