Question

15．如图，△ABC中，∠B，∠C的平分线交于O点，过O点作EF∥BC交AB，AC于E，F．

（1）如图①，当AB=AC时，图中有5个等腰三角形．
（2）如图②，写出EF与BE、CF之间关系式，并说明理由．
（3）如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F． EF与BE、CF关系又如何？说明你的理由．

Answer 1

分析 （1）由AB=AC，可得∠ABC=∠ACB；又已知OB、OC分别平分∠ABC、∠ACB；故∠EBO=∠OBC=∠FCO=∠OCB；根据EF∥BC，可得∠OEB=∠OBC=∠EBO，∠FOC=∠FCO=∠BCO；由此可得出△ABC，△OBC，△EBO，△CFO，△AEF都是等腰三角形；
（2）由EF∥BC，可得∠2=∠3，又∠1=∠2，根据等量代换得到∠1=∠3，所以OE=BE，在△CFO中，同理可证OF=CF，继而可证得EF=BE+CF；
（3）由于OE∥BC，可得∠5=∠6，又∠4=∠5，根据等量代换得到∠4=∠6，所以OE=BE，在△CFO中，同理可证OF=CF，继而可证得EF=BE-CF．

解答 解：（1）当AB=AC时，图中有5个等腰三角形．
如图1，由AB=AC，可得∠ABC=∠ACB，
又∵OB、OC分别平分∠ABC、∠ACB，
∴∠EBO=∠OBC=∠FCO=∠OCB，
根据EF∥BC，可得∠OEB=∠OBC=∠EBO，∠FOC=∠FCO=∠BCO，
由此可得出△ABC，△OBC，△EBO，△CFO，△AEF都是等腰三角形．
故答案为：5；

（2）关系式：EF=BE+CF
如图，∵EF∥BC，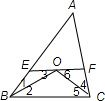
∴∠2=∠3，
又∵∠1=∠2，
∴∠1=∠3，
∴OE=BE，
在△CFO中，同理可证OF=CF，
∵EF=EO+FO，
∴EF=BE+CF；

（3）关系式：EF=BE-CF
如图，∵OE∥BC，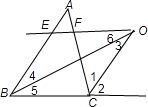
∴∠5=∠6，
又∠4=∠5，
∴∠4=∠6，
∴OE=BE，
在△CFO中，同理可证OF=CF，
∵EF=EO-FO，
∴EF=BE-CF．

点评 本题考查了等腰三角形的判定与性质，解决问题的关键灵活运用等腰三角形的性质．解题时注意：等腰三角形提供了好多相等的线段和相等的角，判定三角形是等腰三角形是证明线段相等、角相等的重要手段．