
分析 (1)根据题意可设m=n2,由最佳分解定义可得F(m)=$\frac{n}{n}$=1;
(2)根据“吉祥数”定义知(10y+x)-(10x+y)=18,即y=x+2,结合x的范围可得2位数的“吉祥数”,求出每个“吉祥数”F(t)的值.
解答 解:(1)对任意一个完全平方数m,设m=n2(n为正整数),
∵|n-n|=0,
∴n×n是m的最佳分解,
∴对任意一个完全平方数m,F(m)=$\frac{n}{n}$=1;
故答案为:1;
(2)设交换t的个位上的数与十位上的数得到的新数为t′,则t′=10y+x,
∵t为“吉祥数”,
∴t′-t=(10y+x)-(10x+y)=9(y-x)=18,
∴y=x+2,
∵1≤x≤y≤9,x,y为自然数,
∴“吉祥数”有:13,24,35,46,57,68,79,
∴所有“吉祥数”中F(t)的值为:F(13)=$\frac{1}{13}$,F(24)=$\frac{4}{6}$=$\frac{2}{3}$,F(35)=$\frac{5}{7}$,F(46)=$\frac{2}{23}$,F(57)=$\frac{3}{19}$,F(68)=$\frac{4}{17}$,F(79)=$\frac{1}{79}$.
点评 本题主要考查了完全平方数以及新定义,理解最佳分解、“吉祥数”的定义,并将其转化为实数的运算是解题的关键.


科目:初中数学 来源: 题型:解答题
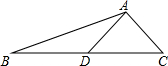 如图,AD是△ABC的中线,tanB=$\frac{1}{4}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.
如图,AD是△ABC的中线,tanB=$\frac{1}{4}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
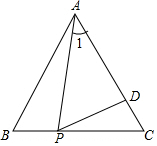 如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$.
如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
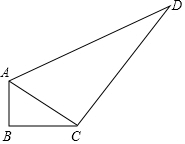 如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠ACD=90°.
如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠ACD=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com