
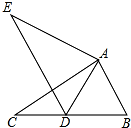
 如图,在△ABC中,∠CAB=95°,AB=3cm,BC=6.2cm,△ABC顺时针旋转一定角度得到△ADE,点D恰好落在BC边上,△ABD为等边三角形.
如图,在△ABC中,∠CAB=95°,AB=3cm,BC=6.2cm,△ABC顺时针旋转一定角度得到△ADE,点D恰好落在BC边上,△ABD为等边三角形.分析 (1)根据旋转的定义进行解答;
(2)先根据旋转的性质得到AD=AB,∠BAD的度数等于旋转角的度数,由于∠B=60°,则可判断△ADB为等边三角形,根据等边三角形的性质得∠BAD=60°,即旋转角的度数为60°,BD=AB=3cm所以CD=BC-BD.
解答 解:(1)∵△ABC绕点A按顺时针旋转一定角度得到△ADE,
∴旋转中心是 点A,∠BAD的度数等于旋转角的度数,
∵△ADB为等边三角形,
∴∠BAD=60°,即旋转角的度数为60°.
故答案是:点A;60°;
(2)∵△ABD为等边三角形,
∴AB=BD=3cm,∠B=60°,
∴∠C=180°-∠CAB-∠B=180°-95°-65°=25°.
∵△ABC顺时针旋转一定角度得到△ADE,
∴∠E=∠C=25°,
∴CD=BC-BD=6.2-3=3.2(cm).
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质.


科目:初中数学 来源: 题型:解答题
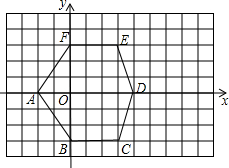 观察图,并回答一下问题:
观察图,并回答一下问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩(百分制) | 面试 | 86 | 92 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com