Question

已知⊙O₁的半径为R，周长为C．
（1）在⊙O₁内任意作三条弦，其长分别是l₁l₂l₃，求证：l₁+l₂+l₃＜C；
（2）如图，在直角坐标系xOy中，设⊙O₁的圆心为O₁（R，R）．
①当直线l：y=x+b（b＞0）与⊙O₁相切时，求b的值；
②当反比例函数y=

k

x

（k＞0）的图象与⊙O₁有两个交点时，求k的取值范围．

Answer 1

分析：（1）根据圆的任意一条弦都小于或等于圆的直径解答；
（2）①设直线与圆相切于点M，连接O₁M，则O₁M⊥l，过点O₁作直线NH⊥x轴，与l交于点N，与x轴交于点H，因为直线的k=1，所以直线与x轴的夹角等于45°，△OMN是等腰直角三角形，点N的坐标即可表示出来，再把点N的坐标代入直线解析式，即可求出b值；
②利用反比例函数图象关于直线y=x对称，作直线y=x的图象与圆有两交点，根据直线与x轴的夹角是45°，用圆的半径表示出两个交点坐标，分别代入反比例函数表达式求出k的值，k的取值就在这两个数值之间．

解答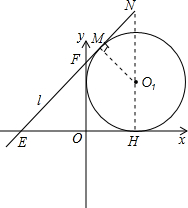：（1）证明：∵l₁≤2R，l₂≤2R，l₃≤2R，
∴l₁+l₂+l₃≤3×2R＜π×2R=C，（2分）
因此，l₁+l₂+l₃＜C．（3分）

（2）解：①如图，根据题意可知⊙O₁与x轴，y轴分别相切，
设直线l与⊙O₁相切于点M，
则O₁M⊥l，过点O₁作直线NH⊥x轴，与l交于点N，与x轴交于点H，
又∵直线l与x轴，y轴分别交于点E（-b，0），F（0，b），
∴OE=OF=b，
∴∠NEO=45°，
∴∠ENO₁=45°，
∴∠NO₁M=45°，
在Rt△O₁MN中，O₁N=O₁M÷sin45°=

2

R．
∴点N的坐标为N（R，

2

R+R），（4分）
把点N坐标代入y=x+b得：

2

R+R=R+b，
解得：b=

2

R．（5分）

②如图，设经过点O，O₁的直线交⊙O₁于点A，D，则由已知，直线OO₁；
y=x是圆与反比例函数图象的对称轴，当反比例函数y=

k

x

的图象与⊙O₁直径AD相交时（点A，D除外），
则反比例函数y=

k

x

的图象与⊙O₁有两个点．
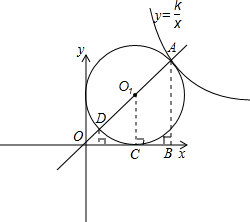
过点A作AB⊥x轴交x轴于点B，过O₁作O₁C⊥x轴于点C，
OO₁=O₁C÷sin45°=

2

R，OA=

2

R+R，
所以OB=AB=OA•sina45°=（

2

R+R）•

2

2

=R+

2

2

R，
因此点A的坐标是A（R+

2

2

R，R+

2

2

R），
将点A坐标代入y=

k

x

，
解得：k=（

3

2

+

2

）R²；（6分）
同理可求得点D的坐标为D（R-

2

2

R，R-

2

2

R），
将点D的坐标代入y=

k

x

，解得：k=（

3

2

-

2

）R²（7分）
所以当反比例函数y=

k

x

（k＞0）的图象与⊙O₁有两个交点时，
k的取值范围是：（

3

2

-

2

）R²＜k＜（

3

2

+

2

）R²．（8分）

点评：本题考查：（1）直径是圆中最长的弦，其它任意弦都小于或等于圆的直径；
（2）一次函数图象的性质和反比例函数图象的性质，结合圆的特点直线的k等于1时与x轴的夹角等于45°是解本题的关键，也是解决本题的突破口．