
����Ŀ������̽�������˽������ձ���Ϊ��ɳĮ֮�ۡ�������������ʱ��ı仯�������ϴ�ı仯���۲�ͼ��ش��������⣺ 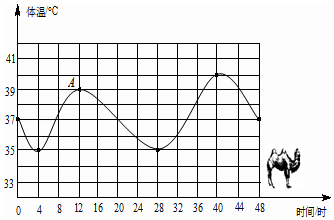
��1��һ���У����յ����µı仯��Χ�� �� �������´���������������Ҫʱ��
��2����16ʱ��24ʱ�����յ������½����ȣ�
��3����ʱ��ʱ�����յ���������������ʱ��ʱ���� ʱ��ʱ���յ��������½���
��4�����ܿ����ڶ���8ʱ���յ��������һ��8ʱ�����µĹ�ϵ�� ��
��5��A���ʾ���� �� ����ʱ���¶���A������ʾ���¶���ͬ��
���𰸡�
��1��35�㡫40�㣻12
��2��3
��3��4��28��12��40��37��12��4��28��40��48
��4����ͬ
��5��12ʱ�����£�44
���������⣺��1��һ���У����յ����µı仯��Χ��35�㡫40�㣬�������´���������������Ҫ12ʱ����2����16ʱ��24ʱ�����յ������½���3�ȣ���3����4��28ʱ��12��40ʱ�����յ���������������37��12ʱ��4��28ʱ����40ʱ��48ʱ���յ��������½�����4�����ܿ����ڶ���8ʱ���յ��������һ��8ʱ�����µĹ�ϵ����ͬ����5��A���ʾ����12���¶ȣ�����44ʱ���¶���A������ʾ���¶���ͬ�� ���Դ��ǣ�35�㡫40�㣬12��16ʱ��24��3��4��28��12��40��37��12��4��28��40ʱ��48����ͬ��12��44��
�����㾫�������պ�����ͼ���ǽ����ĸ�������Ҫ֪��������ͼ������ֱ������ϵ�е�һϵ�е���ɣ�ͼ����ÿһ�����꣨x��y�������˺�����һ�Զ�Ӧֵ�����ĺ�����x��ʾ�Ա�����ij��ֵ��������y��ʾ������Ӧ�ĺ���ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
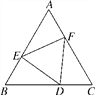
����Ŀ����ͼ���ڡ�ABC�У���B����C����DΪBC����(B��C�����)�Ķ��㣬��EDF��������AB��AC�ֱ��ڵ�E��F����BD��CF��BE��CD.
(1)��֤��DE��DF��
(2)����EDF��m���ú�m�Ĵ���ʽ��ʾ��A�Ķ�����
(3)����EF����DEFΪ�ȱ�������ʱ��A�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У���A=30�㣬��P�ӵ�A������2cm/s���ٶ�������A��C��B�˶�����Q�ӵ�A������a(cm/s)���ٶ���AB�˶���P��Q����ͬʱ��������ijһ���˶�����Bʱ������ͬʱֹͣ�˶�.���˶�ʱ��Ϊx(s)����APQ�����Ϊy(cm2)��y����x�ĺ���ͼ����C1 �� C2������ɣ���ͼ2��ʾ.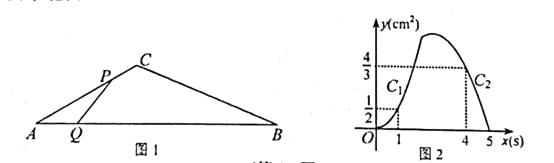
��1����a��ֵ��
��2����ͼ2��ͼ��C2�εĺ�������ʽ��
��3������P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ���������x��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
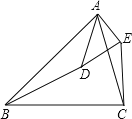
����Ŀ����ͼ������ABC����ADE�У���BAD=��CAE����ABC=��ADE��
��1����֤����ABC�ס�ADE��
��2���ж���ABD����ACE�Ƿ����ƣ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=4cm��AD=12cm��P����AD������ÿ��1cm���ٶȴ�A��D�˶�����Q��BC���ϣ���ÿ��4cm���ٶȴ�C���������CB�������˶�������ͬʱ��������P�㵽��D��Ϊֹ�������ʱ���ڣ��߶�PQ�У� ����ƽ����AB��

A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��BC��OA����B=��A=100�㣬�Իش��������⣺
��1����ͼ�٣���֤��OB��AC�� 
��2����ͼ�ڣ�����E��F���߶�BC�ϣ��������FOC=��AOC������OEƽ�֡�BOF�����EOC�Ķ������������ں��������ϴ𰸼��ɣ��� 
��3���ڣ�2���������£���ƽ���ƶ�AC����ͼ�ۣ���ô��OCB����OFB��ֵ�Ƿ���֮�����仯�����仯����˵�����ɣ������䣬��������ֵ�� 
��4���ڣ�3���������£����ƽ���ƶ�AC�Ĺ����У���ʹ��OEB=��OCA�����OCA������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ӵ�P1����1��0����P2����1����1����P3��1����1����P4��1��1����P5����2��1����P6����2����2������������չ��ȥ����P2017������Ϊ�� ��
A.��504����504��
B.����504��504��
C.����504��503��
D.����505��504��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
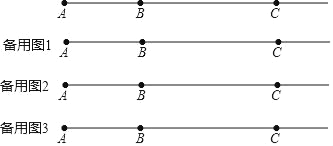
����Ŀ����ͼ��ֱ��l������������A��B��C����AB=8��BC=16����PΪ����AB��һ���㣬���߶�AP���з��۵õ��߶�PA�䣨��A����ֱ��l�ϵ�A�䴦���߶�AP�ϵ����е����߶�PA���ϵĵ��Ӧ����
��1�������ۺ�A��C=2������ǰ�߶�AP=������
��2������P���߶�BC���˶�����MΪ�߶�A��C���е㣬ֱ��д���߶�PM�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧϰ�������ij˷�����ʦ��ͬѧ������һ����Ŀ�����㣺49![]() ������5������˭����ֿ��ֶԣ�����λͬѧ�Ľⷨ���£�
������5������˭����ֿ��ֶԣ�����λͬѧ�Ľⷨ���£�
С����ԭʽ=��![]() ��5=��
��5=��![]() =��249
=��249![]() ��
��
С����ԭʽ=��49+![]() ��������5��=49������5��+
��������5��=49������5��+![]() ������5��=��249
������5��=��249![]() ��
��
��1�������������ֽⷨ������Ϊ˭�Ľⷨ�Ϻã�
��2������Ľⷨ�����к�����������Ϊ���и��õķ���������У������д������
��3��������Ϊ����ʵķ������㣺19![]() ������8��
������8��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com