
 如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.
如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC. 科目:初中数学 来源: 题型:解答题
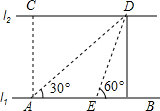 如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.
如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$是无理数 | B. | $\sqrt{8}$的大小介于2和3之间 | ||
| C. | $\sqrt{8}$可以用数轴上的点表示 | D. | $\sqrt{8}$是$\sqrt{2}$的4倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5副 | B. | 6副 | C. | 7副 | D. | 8副 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
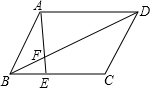 如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )
如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )| A. | 4:5 | B. | 4:9 | C. | 5:9 | D. | 4:10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com