练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．下列关于$\sqrt{8}$的说法中，不正确的是（　　）
    A．$\sqrt{8}$是无理数B．$\sqrt{8}$的大小介于2和3之间
    C．$\sqrt{8}$可以用数轴上的点表示D．$\sqrt{8}$是$\sqrt{2}$的4倍

    分析 根据无理数的定义、无理数的估值、实数和数轴上的点的对应关系及二次根式的化简解答可得．

    解答 解：A、$\sqrt{8}$是无理数，此结论正确；
    B、$\sqrt{4}$＜$\sqrt{8}$＜$\sqrt{9}$，即2＜$\sqrt{8}$＜3，则$\sqrt{8}$的大小介于2和3之间，此结论正确；
    C、$\sqrt{8}$可以用数轴上的点表示，此结论正确；
    D、$\sqrt{8}$=2$\sqrt{2}$，则$\sqrt{8}$是$\sqrt{2}$的2倍，此结论错误；
    故选：D．

    点评 本题主要考查实数，熟练掌握无理数的定义、无理数的估值、实数和数轴上的点的对应关系及二次根式的化简是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

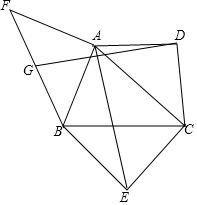    19．如图所示，已知△ABC是锐角三角形，以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE，以边AB为直角边向形外作等腰直角三角形ABF，∠BAF=90°，点G为BF的中点，连接GD和AE，试探究GD和AE的数量关系和位置关系，并对你的结论加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．（a）展开（x-4）3
    （b）由此，因式分解x3-12x2+48x-56．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

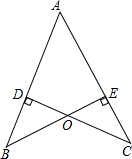    17．如图CD⊥AB于D，BE⊥AC于E，OD=OE，求证：OB=OC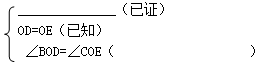   
    证明：
    ∵CD⊥AB，BE⊥AC
    ∴∠ODB=∠OEC=90° （垂直的定义）
    ∵在△BOD和△COE中

    ∴△BOD≌△COE（ASA）
    ∴OB=OC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图所示，OA⊥OB，OA=45cm，OB=15cm，一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O，机器人立即从B处出发以相同的速度匀速直线前进去拦截小球，在点C处截住了小球，求机器人行走的路程BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，已知四边形ABCD是正方形，P是直线AD上一动点，使△PBC是等腰三角形的点P有（　　）
    A．1个B．3个C．5个D．7个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列各组中的两个项不属于同类项的是（　　）
    A．3x2y和-2x2yB．a2和32C．-1和$1\frac{1}{4}$D．-xy和2yx

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，是学校花圃的一角，有的同学为了省时间图方便，在花圃中踩出了一条“捷径”，“捷径”的数学道理是（　　）
    A．两点确定一条直线B．垂线段最短
    C．两点之间，线段最短D．两点之间，直线最短

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列计算正确的是（　　）
    A．$\sqrt{2}+\sqrt{5}=\sqrt{7}$B．$3\sqrt{2}-\sqrt{2}=3$C．（3a）2=9aD．$\frac{3}{{\sqrt{3}}}=\sqrt{3}$

    查看答案和解析>>

    同步练习册答案