
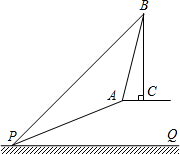
 如图,已知斜坡AP的坡度为i=1:$\sqrt{3}$,坡长AP为20m,与坡顶A处在同-水平面上有-座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角α且tanα=3.求:
如图,已知斜坡AP的坡度为i=1:$\sqrt{3}$,坡长AP为20m,与坡顶A处在同-水平面上有-座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角α且tanα=3.求:分析 (1)作AE⊥PQ于点E,设AE为xm,根据坡度的概念用x表示出PE,根据题意列出方程,解方程即可;
(2)延长BC交PQ于点F,设AC=ym,根据正切的定义表示出BC,根据直角三角形的性质得到BF=PF,列出方程,解方程即可.
解答 解:(1)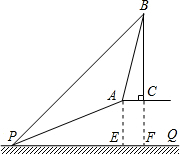 作AE⊥PQ于点E,
作AE⊥PQ于点E,
∵斜坡AP的坡度为i=1:$\sqrt{3}$,
∴$\frac{AE}{PE}$=$\frac{1}{\sqrt{3}}$,
设AE为xm,则PE为$\sqrt{3}$xm,
由勾股定理得,AP=2x,
由题意得2x=20,
解得,x=10,
则AE=10m,PE=10$\sqrt{3}$m,
答:坡顶A到地面PQ的距离为10m;
(2)延长BC交PQ于点F,
设AC=ym,
∵tanα=3,
∴BC=3y,
∵∠BPF=45°,
∴PF=BF,
∴10$\sqrt{3}$+y=3y+10,
解得y=5$\sqrt{3}$-5,
则BC=3y=15$\sqrt{3}$-15.
答:古塔BC的高度为(15$\sqrt{3}$-15)m.
点评 本题考查的是解直角三角形的应用-坡度坡角问题、仰角俯角问题,掌握坡度是坡面的铅直高度h和水平宽度l的比、理解仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
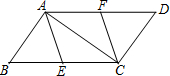 如图,E、F分别是?ABCD的边BC、AD上的中点.
如图,E、F分别是?ABCD的边BC、AD上的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
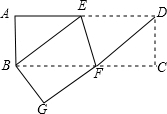 如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE.
如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7.
如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
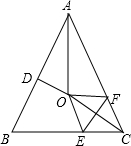 如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°.
如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com