
 如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7.
如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7. 分析 根据折叠的性质可得EF=AE、BF=BA,从而?ABCD的周长可转化为:△FDE的周长+△FCB的周长,求出AB+BC,再由△FCB的周长为22,求出FC的长,即可解决问题.
解答 解:由折叠的性质可得EF=AE、BF=AB,
∴?ABCD的周长=DF+FC+CB+BA+AE+DE=△FDE的周长+△FCB的周长=8+22=30,
∵四边形ABCD为平行四边形,
∴AB+BC=15,
∵△FCB的周长=CF+BC+BF=CF+BC+AB=22,
即FC+15=22,
∴FC=7,
故答案为7.
点评 本题主要考查了翻折变换的性质、平行四边形的性质等几何知识点;根据折叠的性质将平行四边形的周长与△FCB的周长进行转化是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
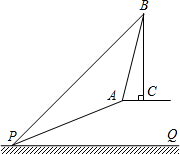 如图,已知斜坡AP的坡度为i=1:$\sqrt{3}$,坡长AP为20m,与坡顶A处在同-水平面上有-座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角α且tanα=3.求:
如图,已知斜坡AP的坡度为i=1:$\sqrt{3}$,坡长AP为20m,与坡顶A处在同-水平面上有-座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角α且tanα=3.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知线段m,∠a(如图).
已知线段m,∠a(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com