
分析 (1)根据差倒数的计算公式分别求解可得;
(2)由(1)得出数列的循环周期为3,据此可得原式=(-$\frac{1}{3}$)×$\frac{3}{4}$×4×(-$\frac{1}{3}$)×$\frac{3}{4}$×4×…×(-$\frac{1}{3}$)×$\frac{3}{4}$×4=$\underset{\underbrace{(-1)×(-1)×…×(-1)}}{672个-1相乘}$,可得答案.
解答 解:(1)根据题意,得:x2=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,x3=$\frac{1}{1-\frac{3}{4}}$=4,x4=$\frac{1}{1-4}$=-$\frac{1}{3}$;
(2)由(1)知,该数列循环周期为3,
∴2016÷3=672,
则x1x2…x2016=(-$\frac{1}{3}$)×$\frac{3}{4}$×4×(-$\frac{1}{3}$)×$\frac{3}{4}$×4×…×(-$\frac{1}{3}$)×$\frac{3}{4}$×4
=$\underset{\underbrace{(-1)×(-1)×…×(-1)}}{672个-1相乘}$
=1.
点评 本题主要考查数字的变化规律,根据题意掌握差倒数的计算公式及数列的变化规律是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
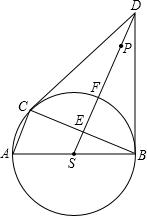 如图,在⊙S中,AB是直径,AC、BC是弦,D是⊙S外一点,且DC与⊙S相切于点C,连接CS,DS,DB,其中DS交BC于点E,交⊙S于点F,F为弧BC的中点.
如图,在⊙S中,AB是直径,AC、BC是弦,D是⊙S外一点,且DC与⊙S相切于点C,连接CS,DS,DB,其中DS交BC于点E,交⊙S于点F,F为弧BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com