
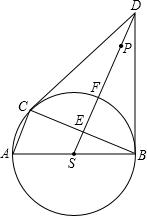
 如图,在⊙S中,AB是直径,AC、BC是弦,D是⊙S外一点,且DC与⊙S相切于点C,连接CS,DS,DB,其中DS交BC于点E,交⊙S于点F,F为弧BC的中点.
如图,在⊙S中,AB是直径,AC、BC是弦,D是⊙S外一点,且DC与⊙S相切于点C,连接CS,DS,DB,其中DS交BC于点E,交⊙S于点F,F为弧BC的中点.分析 (1)根据SAS证明△DCS≌△DBS;
(2))①由(1)得:△DCS≌△DBS,得CD=BD,可知SD是BC的中垂线,所以CE=BE,证明△CSE∽△DSC,列比例式可求得ED的长,则可计算PD的长;
②根据C与B关于SD对称,由最短路径得:当P与S重合时,△PAC的周长最小,如图3,根据①可得PD的长.
解答 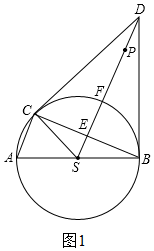 证明:(1)如图1,∵F为弧BC的中点.
证明:(1)如图1,∵F为弧BC的中点.
∴弧FC=弧BF,
∴∠CSF=∠BSF,
∵SC=SB,SD=SD,
∴△DCS≌△DBS(SAS);
(2)①如图2,由(1)得:△DCS≌△DBS,
∴CD=BD,
∵SC=SB,
∴SD是BC的中垂线,
∴CE=BE,
∵AB为⊙S的直径,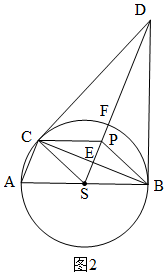
∴∠ACB=90°,
∵AB=10,
∴CS=$\frac{1}{2}$AB=5,
由勾股定理得:BC=8,
∴CE=$\frac{1}{2}$BC=4,
Rt△CSE中,SE=3,
∵四边形PCSB是菱形,
∴PC=CS=5,PE=SE=3,
∵DC与⊙S相切于点C,
∴∠SCD=90°
∴∠SEC=∠SCD=90°,∠CSE=∠CSE,
∴△CSE∽△DSC,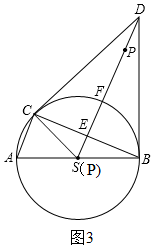
∴$\frac{CS}{DS}=\frac{SE}{CS}$,
∴$\frac{5}{3+ED}=\frac{3}{5}$,
∴ED=$\frac{16}{3}$,
∴PD=$\frac{16}{3}$-3=$\frac{7}{3}$,
则当PD=$\frac{7}{3}$时,四边形PCSB是菱形;
故答案为:$\frac{7}{3}$;
②∵△PAC的周长=AC+PA+PC,
∵AC是定值,
∴当PC+PA的值最小值,△PAC的周长最小,
由①可知:C与B关于SD对称,
∴当P与S重合时,△PAC的周长最小,如图3,
∴PD=ED+SE=$\frac{16}{3}$+3=$\frac{25}{3}$,
即当PD=$\frac{25}{3}$时,△PAC的周长最小.
故答案为:$\frac{25}{3}$.
点评 本题是圆的综合题,考查了圆周角定理、切线的性质、三角形全等和相似的性质和判定、勾股定理、菱形的性质、线段垂直平分线的逆定理等知识,第三问将三角形的周长最小值问题转化为轴对称的最短路径问题解决即可.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com