

分析 (1)①过一点作已知直线的平行线即可;
②根据平行线的性质和三角形内角和定理即可得到∠BAC与∠EFD的数量关系;
(2)首先作出图形,再结合平行线的性质即可得到结论.
解答 解:(1)①见图1;
②∠BAC=∠EFD.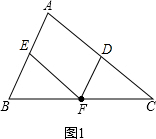
证明:∵EF∥AC,
∴∠EFB=∠C.
∵DF∥AB,
∴∠DFC=∠B.
∴∠EFD=180°-(∠EFB+∠DFC)=180°-(∠C+∠B).
在△ABC中,∠BAC=180°-(∠C+∠B),
∴∠BAC=∠EFD.
(2)当点F在边BC的延长线上时,∠BAC+∠EFD=180°;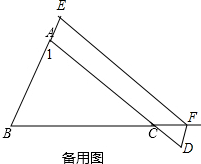
证明:如备用图,
∵DF∥AB,
∴∠D=∠1.
∵EF∥AC,
∴∠EFD+∠D=180°.
∴∠EFD+∠1=180°.
即∠BAC+∠EFD=180°.
点评 本题主要考查了平行线的性质,解题的关键是掌握两直线平行,同位角相等以及两直线平行,同旁内角互补等知识,此题难度不大.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )
甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )| A. | 货车的速度是60千米/小时 | |
| B. | 离开出发地后,两车第一次相遇时,距离出发地150千米 | |
| C. | 货车从出发地到终点共用时7小时 | |
| D. | 客车到达终点时,两车相距180千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(万元/辆) | 售价(万元/辆) | |
| 甲 | 5 | 8 |
| 乙 | 9 | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com