
 如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )| A. | 8 | B. | 4$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | 8$\sqrt{2}$ |
分析 方法一:如图,由题意易证AE=GH=2$\sqrt{5}$,设FH=x,EF=y,则有HE+AG=$\sqrt{{x}^{2}+{y}^{2}}$+$\sqrt{(2\sqrt{5}-x)^{2}+(2\sqrt{5}-y)^{2}}$,欲求HE+AG的最小值,相当于在平面直角坐标系内找一点(x,y),使得这个点到O(0,0),P(2$\sqrt{5}$,2$\sqrt{5}$)的距离和最小,显然这个点在线段OP上,满足x=y时,HE+AG的值最小.想办法求出x的值即可解决问题;
方法二:作GK⊥AB于K,作EM∥AG,GM∥AE,则四边形AEGM是平行四边形.由AG+HE=EM+EG,推出当H、E、M共线时,AG+HE的值最小,最小值=$\sqrt{2}$HG;
解答 解:如图,由题意易证AE=GH=2$\sqrt{5}$,设FH=x,EF=y,则有HE+AG=$\sqrt{{x}^{2}+{y}^{2}}$+$\sqrt{(2\sqrt{5}-x)^{2}+(2\sqrt{5}-y)^{2}}$,
欲求HE+AG的最小值,相当于在平面直角坐标系内找一点(x,y),使得这个点到O(0,0),P(2$\sqrt{5}$,2$\sqrt{5}$)的距离和最小,显然这个点在线段OP上,满足x=y时,HE+AG的值最小,由此可知FH=EF时,HE+AG的值最小,如图连接BD交AE于F,作FM⊥AB于M,FN⊥BC于N,易证△FMH≌△FNE,
∴FH=EF,此时HE+AG的值最小,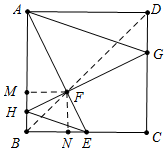
易证四边形BNFM是正方形,设边长为a,则有$\frac{FM}{BE}$=$\frac{AM}{AB}$,
∴$\frac{a}{2}$=$\frac{4-a}{4}$,
∴a=$\frac{4}{3}$,
∴EF=FH=$\sqrt{(\frac{4}{3})^{2}+(\frac{2}{3})^{2}}$=$\frac{2}{3}$$\sqrt{5}$,
∴x=y=$\frac{2}{3}$$\sqrt{5}$,
∴HE+AG的最小值=2$\sqrt{10}$,
故选C.
解法二:作GK⊥AB于K,作EM∥AG,GM∥AE,则四边形AEGM是平行四边形.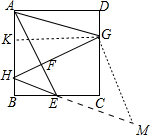
∵AE⊥HG,
∴∠B=∠GKH=∠AFH=90°,
∴∠BAE+∠AHF=90°,∠AHF+∠KGH=90°,
∴∠BAE=∠KGH,
∵KG=BC=AB,
∴△KGH≌△BAE,
∴GH=AG,
∴AE=GM=HG,AG=EM,
∴△GHM是等腰直角三角形,GH=GM=AE=2$\sqrt{5}$,
∵AG+HE=EM+EG,
∴当H、E、M共线时,AG+HE的值最小,最小值=$\sqrt{2}$HG=2$\sqrt{10}$.
故选C.
点评 本题考查轴对称-这个问题、正方形的性质,全等三角形的判定和性质、勾股定理等知识,解题的关键是学会用转化的思想思考问题,学会添加常用辅助线,本题体现了数形结合的思想的应用,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠ACB=135°,AC=4,在同一平面内,将△ABC绕点C顺时针方向旋转到△A′B′C,使得AA′∥CB,则AA′的长度为4$\sqrt{2}$.
如图,△ABC中,∠ACB=135°,AC=4,在同一平面内,将△ABC绕点C顺时针方向旋转到△A′B′C,使得AA′∥CB,则AA′的长度为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
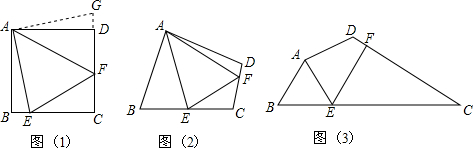
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 55° 或125° | B. | 65° | C. | 55° | D. | 125° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
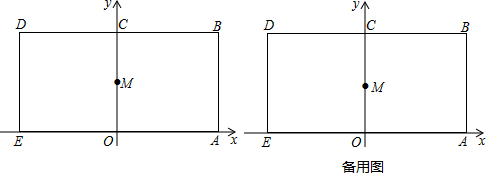
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com