
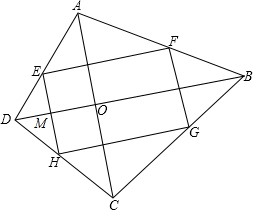
 证明:∵四边形EFGH是矩形,
证明:∵四边形EFGH是矩形,

 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
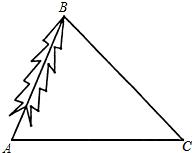 为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
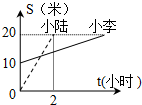 小李和小陆沿同一条路行驶到B地,他们离出发地的距离S和行驶时间t之间的函数关系的图象如图.已知小李离出发地的距离S和行驶时间t之间的函数关系为y=2x+10.则:
小李和小陆沿同一条路行驶到B地,他们离出发地的距离S和行驶时间t之间的函数关系的图象如图.已知小李离出发地的距离S和行驶时间t之间的函数关系为y=2x+10.则:查看答案和解析>>
科目:初中数学 来源: 题型:
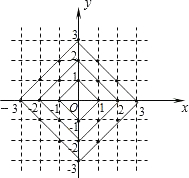 在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点.观察图(4)中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第8个正方形(实线)四条边上的整点个数共有
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点.观察图(4)中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第8个正方形(实线)四条边上的整点个数共有查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com